从[SDOI2011]消耗战开始的虚树学习

发表于 更新于 分类于 ， 阅读次数：

人类今天也在绝赞衰退中！

人类今天也在绝赞衰退中

虚树

浓缩信息，把一整颗大树浓缩成一颗小树 。——$\operatorname{OIwiki}$

用途

虚树是在树形$dp$中使用的一种特殊优化，适用于树中仅有少量关键节点且普通节点很多的情况。可以将关键点和他们的$\operatorname{LCA}$拿出来另建一棵树，并在这棵树上另外进行树形$dp$。

前置技能

邻接表或链式前向星存图、任意一种求$\operatorname{LCA}$的算法、单调栈（这个不会也可以直接学）

步骤

  1. 在原树上进行dfs，进行LCA预处理，同时得到原树上的dfs序，方便之后虚树构造，此外还可以进行一些dp预处理，便于进行虚树上的第二次dp。
  2. 确定关键节点集合，并按照dfs序排序。
  3. 通过单调栈及LCA算法构建出虚树。
  4. 在虚树上进行树形dp求解。

为什么是dfs序

完整问题：为什么将关键节点按$dfs$序排序后，将相邻关键节点的$\operatorname{LCA}$加入得到虚树上的所有结点？
首先任意关键节点都在虚树上，这些关键节点形成的所有$\operatorname{LCA}$也都在虚树上，虚树的叶子一定为关键节点。
不按$dfs$序而缺少$\operatorname{LCA}$的情况如下图所示：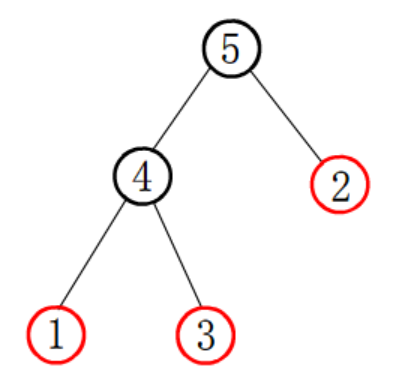
在这里插入图片描述
如果按照字典序加入$lca(1,2)$，$lca(2,3)$，会缺少$lca(1,3)=4$，可以发现因为没有考虑节点1,3和其最近公共祖先4构成的子树。
没有查到可信的证明：在这里立个猜想，按$dfs$序保证优先处理了所有最小子树的$\operatorname{LCA}$，并且加入了所有（关键节点及其$\operatorname{LCA}$构成的）相邻子树的$\operatorname{LCA}$。
emm，这个描述似乎很不清晰，建议画个草图感性理解下。

如何建立

强推这篇博客，讲的很明白
始终用栈维护一条链，表示从虚树的根一直到栈顶元素这一条链，栈中所有元素即为此时虚树在这条链上的节点。
排序后的第一个关键节点无条件加入栈中，剩下的关键节点按$dfs$序依次考虑。设要加入的关键节点为$now$，栈顶节点为$top$，栈中第二个元素为$top-1$，$now$和$top$的最近公共祖先为$lca$，$dfs$序记录在$dfn$数组中。
$lca$不一定在栈中，但显然在$top$到根节点这条链上，所以$dfn[lca]\le dfn[top]$。
插入关键节点$now$时一共有四种情况：

  1. $dfn[lca]=dfn[top]$。即$now$节点在$lca$的子树上，将$now$推入栈中，链端向下延伸即可。
  2. $dfn[lca]>dfn[top-1]$且$dfn[lca]<dfn[top]$。说明$lca$在$top$和$top-1$之间，将边$<lca,top>$加入虚树，$top$出栈，$lca$和$now$入栈。
  3. $dfn[lca]=dfn[top-1]$。说明$lca$即$top-1$，和情况2大同小异。将边$<lca,top>$加入虚树，$top$出栈，$now$入栈。
  4. $dfn[lca]<dfn[top-1]$。不断将边$<top-1,top>$加入虚树，$top$出栈，直至不符合情况4，转入上述三种中的一种进行处理。

看不懂的话点进上面的链接，那个有配图，嘤嘤嘤。

喜闻乐见的代码讲解时间

题目

给出一棵带有边权的$n\le 2.5\times 10^5$节点树和$m\le 5\times 10^5$个询问。
每次询问给出$k$个关键节点，你可以切断一些边，代价即为该边边权，求出节点$1$与所有关键节点都不连接的最小代价，$\sum k_i \le 5\times 10^5$。

思路

考虑直接树形$dp$做法，令$dp[x]$为节点$x$不与子树上$x$所有关键节点连接的最小代价，在$dfs$回溯过程中求解。
则对于$x$所有的子节点$v$，若$v$为关键节点，只能通过断掉连接的边来与$v$隔绝，则$$dp[x]+=w(<u,v>)$$否则比较$x$断掉$v$的连接和$v$与子树上关键节点断掉连接的代价$$dp[x]+=min(w(<u,v>),dp[v])$$
这样的复杂度为$O(mn)$，肯定超时。
所以要用虚树优化，若使用倍增算法求$\operatorname{LCA}$，则整体复杂度$O(n+mklogn)$。
菜鸡只会倍增和树剖，这里使用倍增求$\operatorname{LCA}$，同时在倍增预处理$dfs$中标记了$dfs$序，进行了第一遍的$dp$预处理。
这里的$dp[x]$含义为：根节点（这里为节点$1$）与节点$x$断掉联系的最小代价。
在构建出来的虚树上进行第二次树形$dp$，即可求解，同时在$dfs$回溯过程中取消标记和清空虚树。

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
//#pragma comment(linker, "/STACK:102400000,102400000")
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int>pii;
const int maxn=3e5+10,inf=0x3f3f3f3f,mod=1000000007;
const ll INF=0x3f3f3f3f3f3f3f3f;
void read(){}
template<typename T,typename... T2>inline void read(T &x,T2 &... oth) {
    x=0; int ch=getchar(),f=0;
    while(ch<'0'||ch>'9'){if (ch=='-') f=1;ch=getchar();}
    while (ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    if(f)x=-x;
    read(oth...);
}
struct edge
{
    int v,nex;
    ll w;
    edge(int v=0,ll w=0,int nex=0):
        v(v),w(w),nex(nex){}
} e[maxn<<1];
int head[maxn],cnt=0;
void add(int u,int v,int w=0)
{
    e[++cnt].v=v;
    e[cnt].w=w;
    e[cnt].nex=head[u];
    head[u]=cnt;
}
const int maxl=30;
int gene[maxn][maxl],depth[maxn],lg[maxn],dfn[maxn],tim=0;
ll dp[maxn];
void dfs(int x,int fa)
{
    if(!dfn[x])
        dfn[x]=++tim;
    depth[x]=depth[fa]+1;
    gene[x][0]=fa;
    for(int i=1;(1<<i)<=depth[x];i++)//倍增
        gene[x][i]=gene[gene[x][i-1]][i-1];
    for(int i=head[x];~i;i=e[i].nex)
        if(e[i].v!=fa)
        {
            dp[e[i].v]=min(dp[x],e[i].w);
            dfs(e[i].v,x);//在dfs前后加语句可以求出许多有趣的东西
        }
}
int lca(int x,int y)
{
    if(depth[x]<depth[y])//保证x深度≥y
        swap(x,y);
    while(depth[x]>depth[y])//将x提到同一高度
        x=gene[x][lg[depth[x]-depth[y]-1]];
    if(x==y)//是同一个节点
        return x;
    for(int i=lg[depth[x]];i>=0;i--)
        if(gene[x][i]!=gene[y][i])
        {//二分思想,直到跳到LCA的下面一层
            x=gene[x][i];
            y=gene[y][i];
        }
    return gene[x][0];
}
void init(int s,int n)
{
    depth[s]=1;
    for(int i=1;i<=n;i++)//预处理出log2(i)+1的值
        lg[i]=lg[i-1]+((1<<(lg[i-1]+1))==i);//不要写错
    dfs(s,0);
}
//#define ff first
//#define ss second
int h[maxn],stk[maxn],top=0;
bool key[maxn];
struct edge2
{
    int v,nex;
    edge2(int v=0,int nex=-1):
        v(v),nex(nex){};
} G[maxn<<1];
int head2[maxn],cnt2=0;
void adde(int u,int v)
{
    G[++cnt2].v=v;
    G[cnt2].nex=head2[u];
    head2[u]=cnt2;
}
ll dfs2(int x)
{//和x子树上所有关键点断掉联系的代价
//    printf("!%d!",x);
    ll sum=0,ret=0;
    for(int i=head2[x];~i;i=G[i].nex)
    {//与字数上所有关键节点断掉联系的代价和
        int v=G[i].v;
        sum+=dfs2(v);
    }
    if(key[x])//dp[x]表示节点1与x断掉的最小代价
        ret=dp[x];
    else//可以选择直接和x断掉联系,或者x与子树关键点断掉联系
        ret=min(dp[x],sum);
    key[x]=0;
    head2[x]=-1;
    return ret;
}
signed main()
{
    memset(head,-1,sizeof(head));
    memset(head2,-1,sizeof(head2));
    int n,u,v,w,m,k;
    read(n);
    for(int i=1;i<n;i++)
    {
        read(u,v,w);
        add(u,v,w);
        add(v,u,w);
    }
    dp[1]=INF;
    init(1,n);
    read(m);
    while(m--)
    {//m轮,k个资源丰富的点
        read(k);
        for(int i=1;i<=k;i++)
        {
            read(h[i]);
            key[h[i]]=1;
        }
        sort(h+1,h+k+1,[](const int &x,const int &y){
                return dfn[x]<dfn[y];//按dfs序排序
            });
        stk[top=1]=h[1];
        cnt2=0;
        for(int i=2;i<=k;i++)
        {
            int now=h[i];
            int lc=lca(now,stk[top]);
            while(top>1&&dfn[lc]<=dfn[stk[top-1]])//情况4,=是情况3
            {//不断将top送入虚树
                adde(stk[top-1],stk[top]);
                top--;
            }
            if(dfn[lc]<dfn[stk[top]])//情况2
            {//加边,top出栈,lc和now入栈
                adde(lc,stk[top]);
                stk[top]=lc;
            }//否则为情况1
            stk[++top]=now;
        }
        while(--top)
            adde(stk[top],stk[top+1]);
        printf("%lld\n",dfs2(stk[1]));//最后还会剩一个虚根节点
    }
    return 0;
}