这里记录了图论方面平时个人常用的代码模板。
图论
常见概念
- 简单图:不含有平行边和自环的图。
- 多重图:含有平行边(同向)的图。
- 完全图:每一对节点之间都有边的简单图,$n$个节点无向完全图记为$K_n$。
- 平面图:能将所有点和边画在平面上,且边与边不相交的无向图。
- 补图:由$G$中所有节点和所有能使$G$成为完全图的添加边组成的图。
- 生成子图(Spanning Subgraph):含有原图$G$中所有结点的子图。
- 图同构的必要条件:
- 节点数相同。
- 边数相同。
- 度数相同的结点数相同。
网络流常用概念
- 连通图:只有一个连通分支(极大连通子图)的图。
- 割点:无向连通图中一个顶点$v$,,若删除它以及关联的边后,得到的新图至少包含两个连通分支。
- 桥:无向连通图中的一条边$e$,删除它得到的新图包含两个连通分量。
- 团(Clique):原图$G$的一个完全子图。
- 极大团(Maximal Clique):不是其它团的子图的团。
- 最大团(Maximum Clique):顶点最多的极大团。
- 诱导子图(Induced Subgraph):所有节点在原图$G$上连接的边都被包含在内的子图。
- 独立集:在图上选出一些节点,这些节点间两两无边的点集。
- 路径覆盖:在图中找一些路径,这些路径覆盖图中所有的顶点,每个顶点都只与一条路径相关联。
- 最小染色数:用最少的颜色个数给点染色且任意两点相邻点颜色不同,最少的颜色个数。
弦图常用概念
- 弦:连接环上两个不相邻节点的边。
- 弦图:图上任意一个点数大于三的环都至少存在一条弦的无向图。
- 单纯点:节点$v$与相邻节点的诱导子图是一个团。
- 完美消除序列:有$n$个点的排列$v_1,v_2,\dots,v_n$,该排列满足$v_i$在${v_i,v_{i+1},\dots,v_n}$的诱导子图中是一个单纯点。
- 一个无向图是弦图当且仅当它有一个完美消除序列
常见结论
- 每个图中节点度数和等于边数的二倍,$\sum\limits_{v\in V} deg(v)=2\left| E \right|$。
- 任何图中度数为奇数的节点必定有偶数个。
- 完全图$K_n$的边数$=\frac{n(n-1)}{2}$
- 最大团中顶点数量 = 补图的最大独立集中顶点数量
- 最大团数 ≤ 最小染色数,最大独立集 ≤ 最小团覆盖
- 弦图中:最大团数 = 最小染色数,最大独立集 = 最小团覆盖
- 平面图边数$m\le 3n-6$。
弦图
最大势算法求消除序列并判定弦图
判断一个消除序列是否为完美消除序列:从后向前枚举序列中的点$v_i$,设序列中在$v_i$后且与$v_i$相邻的点集依次为${v_{j1},v_{j2},\dots,v_{jk}}$,判断$v_j1$是否与${v_{j2},\dots,v_{jk}}$相邻即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
| #include<bits/stdc++.h>
using namespace std;
const int maxn=1005;
struct edge
{
int v,nex;
edge(int v=0,int n=-1):
v(v),nex(n){}
} e[maxn*maxn];
int cnt=0,head[maxn];
inline void add(int u,int v)
{
e[++cnt].v=v;
e[cnt].nex=head[u];
head[u]=cnt;
}
int label[maxn],id[maxn],order[maxn];
bool vis[maxn];
vector<int> vec[maxn];
void mcs(int n)
{
memset(vis,0,sizeof(vis));
memset(label,0,sizeof(label));
for(int i=1;i<=n;i++)
vec[0].push_back(i);
int maxx=0,now=0;
for(int i=1;i<=n;i++)
{
bool flag=0;
while(!flag)
{
for(int j=vec[maxx].size()-1;j>=0;j--)
{
if(vis[vec[maxx][j]])
vec[maxx].pop_back();
else{
flag=1;
now=vec[maxx][j];
break;
}
}
if(!flag)
maxx--;
}
vis[now]=1;
order[n-i+1]=now;
id[now]=n-i+1;
for(int j=head[now];~j;j=e[j].nex)
{
int v=e[j].v;
if(!vis[v])
{
label[v]++;
vec[label[v]].push_back(v);
maxx=max(maxx,label[v]);
}
}
}
}
int bucket[maxn];
bool isperfect(int n)
{
mcs(n);
memset(vis,0,sizeof(vis));
for(int i=n;i>0;i--)
{
int tot=0,ret=1;
for(int j=head[order[i]];~j;j=e[j].nex)
if(id[e[j].v]>i)
vis[bucket[++tot]=e[j].v]=1;
for(int j=head[bucket[1]];~j;j=e[j].nex)
{
int v=e[j].v;
if(v!=bucket[1]&&vis[v])
{
ret++;
}
}
for(int j=1;j<=tot;j++)
vis[bucket[j]]=0;
if(tot&&ret!=tot)
return 0;
}
return 1;
}
int main()
{
int n,m,u,v;
while(cin>>n>>m&&n&&m)
{
memset(head,-1,sizeof(head));
memset(order,0,sizeof(order));
cnt=0;
for(int i=1;i<=n;i++)
vec[i].clear();
for(int i=1;i<=m;i++)
{
cin>>u>>v;
add(u,v);
add(v,u);
}
cout<<(isperfect(n)?"Perfect\n\n":"Imperfect\n\n");
}
return 0;
}
|
三元环
步骤
- 对原无向图进行定向,对任何一条边,从度数大的点连向度数小的点,如果度数相同,从编号小的点连向编号大的点。得到一个有向无环图。
- 枚举每一个节点$u$,将$u$所有相邻节点打上$u$的标记。再枚举$u$的相邻节点$v$,枚举$v$的相邻节点的相邻节点$w$,如果$w$上有被标记为$u$,则$(u,v,w)$就是一个三元环。
统计图上三元环数量,复杂度$O(m\sqrt{m})$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| vector G[maxn];
int vis[maxn],deg[maxn];
int cycle3(int n)
{
int ans=0;
for(auto &e:edges)
{
deg[e.u]++;
deg[e.v]++;
}
for(auto &e:edges)
if(deg[e.u]<deg[e.v]||(deg[e.u]==deg[e.v]&&e.u<e.v))
G[e.u].push_back(edge(e.u,e.v));
else
G[e.v].push_back(edge(e.v,e.u));
for(int u=1;u<=n;u++)
{
for(int v:G[u])
vis[v]=u;
for(int v:G[u])
for(int w:G[v])
if(vis[w]==u)
ans++;
}
return ans;
}
|
最短路
Dijkstra堆优化
复杂度$O(ElgE)$,稠密图中有时不如普通版优秀,但比SPFA快。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| const int MAXN=1050;
struct qnode{
int v,c;
qnode(int _v=0,int _c=0):v(_v),c(_c){}
bool operator <(const qnode &r)const{
return c>r.c;
}
};
struct Edge{
int v,cost;
Edge(int _v=0,int _cost=0):v(_v),cost(_cost){}
};
vector<Edge>E[MAXN];
bool vis[MAXN];
int dist[MAXN];
void Dijkstra(int n,int start)
{
memset(vis,false,sizeof(vis));
for(int i=1;i<=n;i++)
dist[i]=inf;
priority_queue<qnode>que;
while(!que.empty())
que.pop();
dist[start]=0;
que.push(qnode(start,0));
while(!que.empty())
{
qnode now=que.top();
que.pop();
int u=now.v;
if(vis[u])
continue;
vis[u]=true;
for(int i=0;i<E[u].size();i++)
{
int v=E[u][i].v;
int cost=E[u][i].cost;
if(!vis[v]&&dist[v]>dist[u]+cost){
dist[v]=dist[u]+cost;
que.push(qnode(v,dist[v]));
}
}
}
}
void addedge(int u,int v,int w)
{
E[u].push_back(Edge(v,w));
}
|
SPFA
最坏复杂度$O(VE)$,V为节点数,不适用于稠密图
检测负环:当存在一个点入队大于等于$V$次,则有负环
BFS实现(求最短路)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| const int inf=0x3f3f3f3f,MAXN=5051;
struct node
{
int v,w,next;
} e[MAXN];
int cnt,dist[MAXN],head[MAXN],num[MAXN];
bool vis[MAXN];
void add(int u,int v,int w)
{
e[cnt].v=v;
e[cnt].w=w;
e[cnt].next=head[u];
head[u]=cnt++;
}
bool SPFA(int n,int x)
{
memset(dist,inf,sizeof(dist));
memset(vis,0,sizeof(vis));
memset(num,0,sizeof(num));
dist[x]=0;
num[x]++;
queue<int> QAQ;
QAQ.push(x);
while(!QAQ.empty())
{
int now=QAQ.front();
QAQ.pop();
vis[now]=0;
for(int i=head[now];i!=-1;i=e[i].next)
{
int to=e[i].v;
if(dist[to]>dist[now]+e[i].w)
{
dist[to]=dist[now]+e[i].w;
if(!vis[to])
{
vis[to]=1;
QAQ.push(to);
num[to]++;
if(num[to]>n)
return 1;
}
}
}
}
return 0;
}
|
DFS优化(负环检测)
请先用前向星加边。因为图有可能不连通,检测负环要枚举每个起点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| bool spfa(int x)
{
vis[x]=1;
for(int i=head[x];~i;i=e[i].next){
int v=e[i].v;
if(dist[v]>dist[x]+e[i].w)
{
dist[v]=dist[x]+e[i].w;
if(vis[v])
return 0;
if(!spfa(v))
return 0;
}
}
vis[x]=0;
return 1;
}
|
线段树优化建图
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
| struct edge
{
int v,w;
edge(){}
edge(int v,int w):
v(v),w(w){}
bool operator < (const edge &y)const
{
return w>y.w;
}
};
vector<edge>G[maxn];
inline void adde(int u,int v,int w)
{
G[u].push_back(edge(v,w));
}
int n,shift;
void build(int x,int l,int r)
{
if(l==r)
{
adde(x,l+2*shift,0);
adde(l+2*shift,x,0);
adde(x+shift,l+2*shift,0);
adde(l+2*shift,x+shift,0);
return;
}
adde(x<<1,x,0);
adde(x<<1|1,x,0);
adde(x+shift,x*2+shift,0);
adde(x+shift,x*2+1+shift,0);
int mid=(l+r)>>1;
build(x<<1,l,mid);
build(x<<1|1,mid+1,r);
}
void add(int p,int l,int r,int nl,int nr,int x,int w,bool in)
{
if(nl>r||nr<l)
return;
if(l<=nl&&nr<=r)
{
if(in)
return adde(x+2*shift,p+shift,w);
else
return adde(p,x+2*shift,w);
}
int mid=(nl+nr)/2;
add(p<<1,l,r,nl,mid,x,w,in);
add(p<<1|1,l,r,mid+1,nr,x,w,in);
}
int dist[maxn];
void dijkstra(int s)
{
for(int i=1;i<=n+2*shift;i++)
dist[i]=INF;
vector<bool> vis(n+2*shift+1,false);
priority_queue<edge>q;
q.push(edge(s,0));
while(!q.empty())
{
edge now=q.top();
int x=now.v;
q.pop();
if(vis[x])
continue;
vis[x]=1;
dist[x]=now.w;
for(edge &i:G[x])
{
if(!vis[i.v]&&dist[i.v]>dist[x]+i.w)
{
dist[i.v]=dist[x]+i.w;
q.push(edge(i.v,dist[i.v]));
}
}
}
}
signed main(signed argc, char const *argv[])
{
int q,s,ope,u,v,w,l,r;
cin>>n>>q>>s;
shift=4*n;
build(1,1,n);
for(int i=1;i<=q;i++)
{
cin>>ope;
if(ope==1)
{
cin>>u>>v>>w;
adde(u+2*shift,v+2*shift,w);
}
else if(ope==2)
{
cin>>u>>l>>r>>w;
add(1,l,r,1,n,u,w,1);
}
else{
cin>>u>>l>>r>>w;
add(1,l,r,1,n,u,w,0);
}
}
dijkstra(s+2*shift);
for(int i=1;i<=n;i++)
cout<<(dist[i+2*shift]==INF?-1:dist[i+2*shift])<<' ';
return 0;
}
|
Floyd
1
2
3
4
5
6
7
8
9
10
11
| long long path[805][805];
void floyd(int n)
{
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(path[i][k]+path[k][j]<path[i][j])
{
path[i][j]=path[i][k]+path[k][j];
}
}
|
Floyd求最小环
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| int dp[maxn][maxn],mp[maxn][maxn];
signed main()
{
int n,m,u,v,d;
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
dp[i][j]=mp[i][j]=(i==j?0:inf);
for(int i=1;i<=m;i++){
cin>>u>>v>>d;
dp[u][v]=dp[v][u]=mp[u][v]=mp[v][u]=min(dp[u][v],d);
}
int ans=inf;
for(int k=1;k<=n;k++){
for(int i=1;i<k;i++)
for(int j=i+1;j<k;j++)
ans=min(ans,dp[i][j]+mp[i][k]+mp[k][j]);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]);
}
if(ans==inf) cout<<"No solution."<<endl;
else cout<<ans<<endl;
return 0;
}
|
最大团
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
| #include<bits/stdc++.h>
using namespace std;
const int maxn=60;
int G[maxn][maxn],tmp[maxn][maxn];
int n,ans,tot,f[maxn];
stack<int>stk,rec;
bool dfs(int dep,int num)
{
if(num==0)
{
if(dep>ans)
{
ans=dep;
rec=stk;
return 1;
}
return 0;
}
for(int i=1;i<=num;i++)
{
if(dep+num-i+1<=ans)
return 0;
int v=tmp[dep][i];
if(dep+f[v]<=ans)
return 0;
int cnt=0;
for(int j=i+1;j<=num;j++)
{
int vv=tmp[dep][j];
if(G[v][vv])
tmp[dep+1][++cnt]=vv;
}
stk.push(v);
if(dfs(dep+1,cnt))
return 1;
stk.pop();
}
return 0;
}
int maxClique(int n)
{
if(n==0)
return 0;
memset(f,0,sizeof(f));
f[n]=ans=1;
for(int i=n-1;i>=1;i--)
{
tot=0;
while(!stk.empty())
stk.pop();
stk.push(i);
for(int j=i+1;j<=n;j++)
if(G[i][j])
tmp[1][++tot]=j;
dfs(1,tot);
f[i]=ans;
}
return ans;
}
int main()
{
scanf("%d",&n);
int u,v;
while(~scanf("%d%d",&u,&v))
G[u][v]=G[v][u]=1;
printf("%d\n",maxClique(n));
return 0;
}
|
差分约束
定义
如果一个系统是由n个变量和m个约束条件组成,并且每个约束条件能够形成形如$x_i−x_j\le c_k$的形式,我们就称该系统为差分约束系统。
解法
我们如果要求$x_n-x_1$的最大值,先将不等号方向统一,统一为$x_i−x_j\le c_k$形式时,从$x_j$向$x_i$连一条权值为$c_k$的边,跑从$x_1$到$x_n$的最短路,$dist(x_n)-dist(x_1)$即为所求答案。
如果求某两个变量的差的最小值(或者让一组解中最大值最小),那么将所有等式转换为$x_j−x_i\ge -c_k$,从$x_i$向$x_j$连一条权值为$-c_k$的边,跑最长路,$dist$数组即为此时的答案。
因为可能会出现负环,此时无解,所以要使用SPFA求解,建立一个超级源点并向所有点连一条$0$费用的单向边,最坏复杂度$O(nm)$。
例题
CF1131D Gourmet choice:留待研究,$x_i - x_j \ge c_k$的建图跑最长路。
CF1450E Capitalism:连通图上$n$个点,有$m$个关系,关系可以视为边,有如下两种。询问是否存在一种方案,使得存在关系的两个边的值不相等,若存在则输出使图上最大权值最大化的方案。
思路:要使权值最大化,跑最短路,因为不确定以哪个点为起点能使最大距离最大,所以以每个点为起点都跑一遍并记录。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
| vector<edge>G[maxn];
ll dist[maxn],ans=-inf,pos=0;
vector<pii>rec;
bool spfa(int n,int st)
{
vector<bool>vis(n+2,false);
vector<int>cnt(n+2,0);
queue<int>QAQ;
for(int i=1;i<=n;i++)
dist[i]=INF;
QAQ.push(st);
cnt[st]++;
dist[st]=0;
while(!QAQ.empty())
{
int u=QAQ.front();
QAQ.pop();
vis[u]=0;
for(auto &e:G[u])
if(dist[e.v]>dist[u]+e.w)
{
dist[e.v]=dist[u]+e.w;
if(!vis[e.v])
{
if(++cnt[e.v]>n+1)
return true;
vis[e.v]=1;
QAQ.push(e.v);
}
}
for(pii &i:rec)
if(dist[i.ff]==dist[i.ss])
return true;
for(int i=1;i<=n;i++)
if(dist[i]>ans)
{
ans=dist[i];
pos=st;
}
return false;
}
signed main(signed argc, char const *argv[])
{
int n,m,u,v,w;
cin>>n>>m;
for(int i=1;i<=m;i++)
{
cin>>u>>v>>w;
if(w==1)
{
G[u].push_back(edge(v,1));
G[v].push_back(edge(u,-1));
}
else{
G[u].push_back(edge(v,1));
G[v].push_back(edge(u,1));
rec.push_back(pii(u,v));
}
}
for(int i=1;i<=n;i++)
if(spfa(n,i))
return cout<<"NO"<<endl,0;
spfa(n,pos);
cout<<"YES"<<endl;
cout<<ans<<endl;
for(int i=1;i<=n;i++)
cout<<dist[i]<<' ';
return 0;
}
|
最小生成树(MST)
Prim算法
复杂度:邻接矩阵:$O(V^2)$,邻接表:$O(ElogV)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| const int inf=0x3f3f3f3f,maxn=105;
int dist[maxn][maxn],closest[maxn],lowcost[maxn];
bool tree[maxn];
int prim(int n,int u0)
{
memset(tree,0,sizeof(tree));
tree[u0]=1;
int i,j;
for(i=1;i<=n;i++)
if(i!=u0){
lowcost[i]=dist[u0][i];
closest[i]=u0;
}
else
lowcost[u0]=0;
for(i=1;i<=n;i++)
{
int temp=inf,t;
for(j=1;j<=n;j++)
{
if(!tree[j]&&lowcost[j]<temp)
{
t=j;
temp=lowcost[j];
}
}
if(t==u0)
break;
tree[t]=1;
for(j=1;j<=n;j++)
{
if(!tree[j]&&dist[t][j]<lowcost[j])
{
lowcost[j]=dist[t][j];
closest[j]=t;
}
}
}
int ans=0;
for(i=1;i<=n;i++)
ans+=lowcost[i];
return ans;
}
|
Kruskal
使用并查集优化,复杂度$O(mlogm)$
这个不能忘吧……就先不贴了
Boruvka
因为没有$kruskal$好写,所以一般不用于MST裸题。
适于处理边权由连接的两个点的点权通过某种计算方式得出的情况。
平均 $O(V+E)$,最坏 $O((V+E)logV)$。
流程
对每个连通块,处理出与其他连通块连接的最小代价,并记录这条边。
连接所有连通块与其最小连接代价的连通块,并将该边边权计入。
若剩余连通块数量大于1,重复上述步骤。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| struct edge{
int u,v,w;
};
vector<edge> E;
int boruvka(int n)
{
for(int i=1;i<=n;i++)
fa[i]=i;
int ans=0;
vector<int> cost(n+1),rec(n+1);
vector<bool> vis(E.size(),false);
while(1)
{
for(int i=1;i<=n;i++)
cost[i]=inf;
int cur=0;
for(int i=0;i<E.size();i++)
{
int a=findfa(E[i].u),b=findfa(E[i].v),w=E[i].w;
if(a==b)
continue;
cur++;
if(w<cost[a])
cost[a]=w,rec[a]=i;
if(w<cost[b])
cost[b]=w,rec[b]=i;
}
if(cur==0)
break;
for(int i=1;i<=n;i++)
{
if(cost[i]<inf&&!vis[rec[i]])
{
Merge(E[rec[i]].u,E[rec[i]].v);
ans+=E[rec[i]].w;
vis[rec[i]]=true;
}
}
}
return ans;
}
|
典型例题
题意
$n$节点无向完全图,每个点有点权$a_i$,连接点$i$与点$j$的边的边权为$a_i \oplus a_j$,求这个图的MST的权值,$1\le n \le 2\times 10^5, 0\le a_i \le 2^{30}$。
思路
异或最值问题,套一个trie,如果对这个套路不熟悉,请先做CF923C Perfect Security。
虽然已经没了Borůvka的形但是思想还在。
首先我们对所有点权排序并去重,因为相同的值异或为0,在图中必然是这些点相连且没有贡献,所以我们不用考虑这部分。
将剩下的点权插入trie,从根节点到叶子的一条路径就代表一个点权,叶子结点的数量就代表点权的数量。
初始时每个叶子都代表一个连通块,求解这个问题就是不断连接这些连通块的过程。
对于trie上的节点$x$,如果其左右子树都存在,那么就必须找一条边连接其左右子树,若$x$的所处位数为$w$,则这条边必有$1<<w$的贡献,对于$w$之前的位数,因为$x$到根节点路径相同异或值都为0;对于$[w-1,0]$的位数,这部分的贡献要对trie进行搜索来得到。
此时$x$左右子树已经联通,回溯继续向上处理即可。
$check$最坏情况下一次遍历整个trie树,$O(nlogn)$,最多合并$nlogn$次。
整体时间复杂度$O(nlog^2n)$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
| #include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int inf=0x3f3f3f3f,mod=1000000007;
const int maxn = 200005, M = 2;
int val[maxn],trie[maxn<<5][M],siz[maxn<<5],tot;
void init()
{
tot=1;
}
void Insert(const int key)
{
int rt=0;
for(int i=30;i>=0;i--)
{
int id = (key>>i)&1;
if(!trie[rt][id])
trie[rt][id]=tot++;
rt = trie[rt][id];
}
}
ll check(int x,int y,int w)
{
ll ret=LLONG_MAX;
if(trie[x][0]&&trie[y][0])
ret=min(ret,check(trie[x][0],trie[y][0],w-1));
if(trie[x][1]&&trie[y][1])
ret=min(ret,check(trie[x][1],trie[y][1],w-1));
if(ret==LLONG_MAX)
{
if(trie[x][0]&&trie[y][1])
ret=min(ret,check(trie[x][0],trie[y][1],w-1))+(1<<w);
if(trie[x][1]&&trie[y][0])
ret=min(ret,check(trie[x][1],trie[y][0],w-1))+(1<<w);
if(ret==LLONG_MAX)
return 0;
}
return ret;
}
ll dfs(int x,int w)
{
if(w<0)
return 0;
if(trie[x][0]&&trie[x][1])
return (1<<w)+check(trie[x][0],trie[x][1],w-1)+dfs(trie[x][0],w-1)+dfs(trie[x][1],w-1);
else if(trie[x][0])
return dfs(trie[x][0],w-1);
else
return dfs(trie[x][1],w-1);
}
signed main(int argc, char const *argv[])
{
int n,ans=0;
init();
cin>>n;
for(int i=1;i<=n;i++)
cin>>val[i];
sort(val+1,val+n+1);
n=unique(val+1,val+n+1)-val-1;
for(int i=1;i<=n;i++)
Insert(val[i]);
cout<<dfs(0,30)<<endl;
return 0;
}
|
次小生成树
严格次小生成树(洛谷P4180)
建立最小生成树MST,倍增维护MST上任一点到LCA最大值与次大值。
记录树的重量val,并对边集中选中边进行标记。倍增算出每个节点到祖先的路径最大边与严格次大边权值。枚举每一条不在MST上的的边u->v(权值w),分别计算新树上u->lca(u,v)与v->lca(u,v)的路径最大边权M与严格次大边权m,记录最小非零增量inc=w-M(当M==w时inc=w-m)。最后val+inc即为次小生成树重量。
复杂度瓶颈在排序,$O(mlogm)$
有向图最小生成树(MDST,最小树形图)
树形图:有向图$G=(V,E)$中,选定根节点$root$,$G$的一个以$root$为根节点的子图$T$,$T$中$root$到任意其他节点路径存在且唯一。则$T$称为有向图生成树/树形图DST。
最小树形图:带权有向图$G=(V,E,w)$中边权总和最小的DST,即Minimum Directed Spanning Trees。
特点:
- MDST上一定有且仅有$n-1$条边
- 根节点入度为0,其他节点入度为1
朱刘算法(Edmonds 算法)
流程
- 对每个非根节点,找出权值最小的入边(n-1条),记为集合$E$。若$E$不存在,则MDST一定不存在。
- 判断E中是否成环,成环转到步骤3,否则转到步骤4。
- 若成环则进行缩点,同时更新指向该环的所有边的权值,此更新等效于删去环上的一条边。
- 记该环为$C$,在新图$G_1$中收缩为点$u$,则对于在$G$图中不在环上的且指向该环上任一点$v$的一条边$<v_1,v>$,该边权值记为$w$,在$G_1$中存在边$<v_1,u>$与之对应,且该边权值$W_{G_1}(<v_1,u>)$=$W_{G}(<v_1,v>)-w$。
- 因为任何一个节点入度都不会大于1,在环$C$上已经为点$v$选择了一条入边,所以要根据改边权值更新其他点$v$入边权值,当接下来选择了其他指向$v$的边时,相当于删去了$C$上指向$v$的边。
- 转到步骤1,直到证明不存在或者求得。
- 不成环则展开收缩点,获得MDST。若仅须获得MDST的权值,则不需要展开。
模板
朱刘算法,不包括展开部分,未优化,复杂度$O(VE)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
| #include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1005,inf=0x3f3f3f3f;
struct edge
{
int u,v,w;
edge(int u,int v,int w):
u(u),v(v),w(w){}
};
vector<edge> G;
int id[maxn],in[maxn],pre[maxn],vis[maxn];
ll zltree(int root,int n)
{
ll ans=0;
while(1)
{
fill(in,in+n+1,inf);
for(auto &e:G)
if(e.u!=e.v&&e.w<in[e.v])
{
pre[e.v]=e.u;
in[e.v]=e.w;
}
for(int i=1;i<=n;i++)
if(i!=root&&in[i]==inf)
return -1;
fill(id,id+n+1,0);
memset(vis,0,sizeof(vis));
int tn=0,v;
in[root]=0;
for(int i=1;i<=n;i++)
{
ans+=in[v=i];
while(vis[v]!=i&&!id[v]&&v!=root)
vis[v]=i,v=pre[v];
if(v!=root&&!id[v])
{
id[v]=++tn;
for(int u=pre[v];u!=v;u=pre[u])
id[u]=tn;
}
}
if(tn==0)
break;
for(int i=1;i<=n;i++)
if(!id[i])
id[i]=++tn;
for(int i=0;i<(int)G.size();)
{
auto &e=G[i];
v=e.v;
e.u=id[e.u],e.v=id[e.v];
if(e.u!=e.v)
e.w-=in[v],i++;
else
{
swap(e,G.back());
G.pop_back();
}
}
n=tn;
root=id[root];
}
return ans;
}
int main()
{
int n,m,r,u,v,w;
cin>>n>>m>>r;
for(int i=1;i<=m;i++)
{
cin>>u>>v>>w;
G.push_back(edge(u,v,w));
}
cout<<zltree(r,n)<<endl;
return 0;
}
|
kruskal重构树
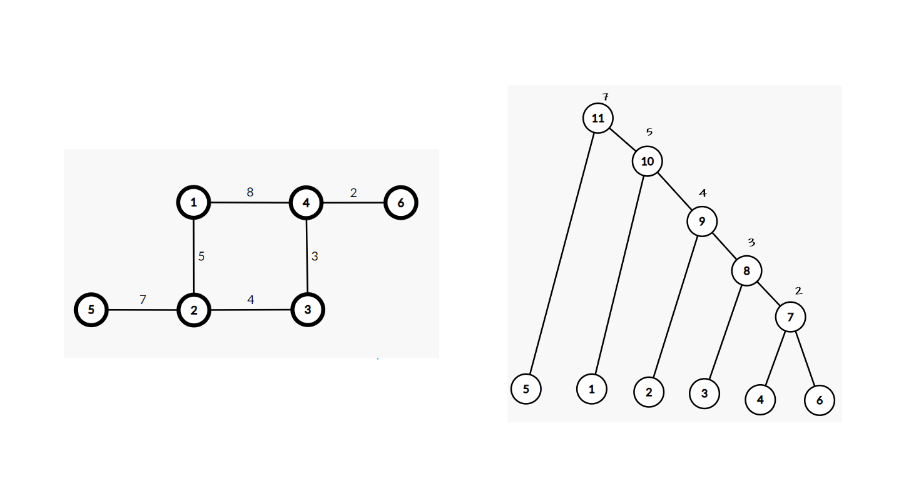
用于求解无向有权图上任意两点$u$到$v$间选择一条路线,使最大边最小化,求该最大边的值。
该值即为$kruskal$重构树上$u$与$v$节点的权值,最小化最大边求值同理。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| for(int i=1;i<=2*n;i++)
fa[i]=i;
int tot=n;
for(auto &e:E)
{
int a=findfa(e.u),b=findfa(e.v);
if(a==b)
continue;
fa[a]=fa[b]=++tot;
val[tot]=e.w;
G[tot].push_back(a);
G[tot].push_back(b);
}
init(tot,tot);
cin>>q;
while(q--)
{
cin>>u>>v;
cout<<val[lca(u,v)]<<'\n';
}
|
矩阵树定理
无向图$G$的生成树个数等于其基尔霍夫矩阵任何一个$n-1$阶主子式的行列式的绝对值(或者任意一个1阶子式的代数余子式)。
基尔霍夫矩阵$K$=度数矩阵$D$−邻接矩阵$A$。
$$
D_{ij}=\begin{cases}deg(v_i)&,v_i=v_j\0&,v_i\ne v_j \end{cases},A_{ij}=\begin{cases}1&,v_i与v_j相接\0&,v_i不与v_j相接 \end{cases},K_{ij}= \begin{cases}deg(v_i)&,i=j\-1&,v_i与v_j相接\0&,v_i与v_j不相接\end{cases}
$$
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| ll Kirchhoff(int n)
{
n--;
ll ans=1;
for(int i=1;i<=n;i++)
{
for(int j=i+1;j<=n;j++)
while(Kir[j][i])
{
ll tmp=Kir[i][i]/Kir[j][i];
for(int k=i;k<=n;k++)
{
Kir[i][k]=(Kir[i][k]-tmp*Kir[j][k]%mod+mod)%mod;
std::swap(Kir[j][k],Kir[i][k]);
}
ans=-ans;
}
ans=(ans*Kir[i][i])%mod;
}
return (ans+mod)%mod;
}
|
扩展
外向树:所有边的方向都是从根指向叶子。
内向树:所有边的方向都是从叶子指向根。
- 内向生成树个数:将度数矩阵换成点的入度。
- 外向生成树个数:将度数矩阵换成点的出度。
虚树
虚树是在树形dp中使用的一种特殊优化,适用于树中仅有少量关键节点且普通节点很多的情况。可以将关键点和他们的LCA拿出来另建一棵树,并在这棵树上另外进行树形dp。
步骤
- 在原树上进行dfs,进行LCA预处理,同时得到原树上的dfs序,方便之后虚树构造,此外还可以进行一些dp预处理,便于进行虚树上的第二次dp。
- 确定关键节点集合,并按照dfs序排序。
- 通过单调栈及LCA算法构建出虚树。
- 在虚树上进行树形dp求解。
代码示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| sort(h+1,h+k+1,[](const int &x,const int &y){
return dfn[x]<dfn[y];
});
stk[top=1]=1;
g[1].clear();
for(int i=1;i<=k;i++)
{
int now=h[i];
int lc=lca(now,stk[top]);
while(top>1&&dfn[lc]<=dfn[stk[top-1]])
{
adde(stk[top-1],stk[top]);
top--;
}
if(dfn[lc]<dfn[stk[top]])
{
g[lc].clear();
adde(lc,stk[top]);
stk[top]=lc;
}
g[now].clear();
stk[++top]=now;
}
while(--top)
adde(stk[top],stk[top+1]);
|
例题
拓扑排序
只适用于DAG。
使用队列(要求字典序时使用优先队列),在邻接表存边时统计每个结点的入度,入度为0则入队。按出队顺序编号,删除以该节点为尾的边,该边边头入度减1,若变为0则入队。直到队列为空,得到top数组与node数组。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| const int maxn=105;
vector<int> G[maxn];
int n,m,top[maxn],node[maxn];
void topsort(void)
{
priority_queue<int,vector<int>,greater<int> > QAQ;
for(int i=1;i<=n;i++)
if(G[i][0]==0)
QAQ.push(i);
int cnt=0;
while(!QAQ.empty())
{
int x=QAQ.top();
top[x]=++cnt;
QAQ.pop();
for(int i=1;i<G[x].size();i++)
{
if(--G[G[x][i]][0]==0)
QAQ.push(G[x][i]);
}
}
if(cnt!=n)
return;
for(int i=1;i<=n;i++)
node[top[i]]=i;
return;
}
int main()
{
while(cin>>n>>m&&(n||m)){
for(int i=1;i<=n;i++){
G[i].clear();
G[i].push_back(0);
}
for(int i=0;i<m;i++){
int u,v;
cin>>u>>v;
G[u].push_back(v);
G[v][0]++;
}
topsort();
}
return 0;
}
|
补图搜索
也是很套路的题了,使用$set$数组来代替邻接表,用$set.find(v)$来确定边是否在图中。并查集、DFS、BFS都可以做。
初始化$ans=0$,并将所有的点放进一个未访问集合$unvis$中,当集合非空时,取出$unvis.begin()$记为$now$并从集合中去掉,并从该点开始BFS,遍历$nuvis$集,并在邻接表$set[now]$中查询,若$set.find()$未找到,则说明该边为补边。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| set<int> G[maxn];
int bfs(int n)
{
int ans=0;
set<int> unvis;
for(int i=1;i<=n;i++)
unvis.insert(i);
while(!unvis.empty())
{
ans++;
int now=*(unvis.begin());
unvis.erase(now);
queue<int> QwQ;
QwQ.push(now);
while(!QwQ.empty())
{
int nex=QwQ.front();
QwQ.pop();
vector<int> v1;
for(auto i:unvis)
if(G[nex].find(i)==G[nex].end())
{
v1.push_back(i);
QwQ.push(i);
}
for(int i=0;i<v1.size();i++)
unvis.erase(v1[i]);
}
}
return ans;
}
|
欧拉路
给定一张联通无向/有向图,求一条经过所有边恰好一次的回路。
有解当且仅当所有点 度数为偶数(无向)/**入度等于出度(有向)**。 任选一点开始dfs,每条边只经过一次。回溯时将回溯的边加入队列,最后队列的逆序就是答案。 时间复杂度$O(m)$。
欧拉路径也可以用一样的方法求出(找度数为奇数的点进行DFS)。
判定
- 无向图欧拉回路:所有点度数都为偶数
- 有向图欧拉回路:所有点入度=出度
- 无向图欧拉路:有0或2个点度数为奇数,其余点度数为偶数
- 有向图欧拉路:一个点入度=出度+1,一个点出度=入度+1,其余点入度=出度
Hierholzer算法
待补…
两笔画问题
有解当且仅当入度为奇数的点不超过四个。 将其中两个点加一条边后求欧拉路径,然后在这条边处断开成两条欧拉路即可。 时间复杂度$O(m)$。
汉密尔顿回路
求简单无向图的环数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| const int maxn=19,inf=0x3f3f3f3f,mod=1000000007;
ll dp[1ll<<maxn][maxn],ans;
vector<int>G[maxn];
signed main(signed argc, char const *argv[])
{
int n,m,u,v;
cin>>n>>m;
for(int i=1;i<=m;i++)
{
cin>>u>>v;
u--,v--;
G[u].push_back(v);
G[v].push_back(u);
}
for(int i=0;i<n;i++)
dp[1ll<<i][i]=1;
#define lowbit(x) ((x) & -(x))
for(int k=1;k<(1ll<<n);k++)
{
for(int x=0;x<n;x++)
{
if(!dp[k][x])
continue;
for(int &v:G[x])
{
if(lowbit(k)>(1ll<<v))
continue;
if(k&(1ll<<v))
{
if(lowbit(k)==(1ll<<v))
ans+=dp[k][x];
}
else
dp[k|(1ll<<v)][v]+=dp[k][x];
}
}
}
cout<<(ans-m)/2<<endl;
return 0;
}
|
强连通分量
Tarjan
Tarjan缩点+DAG 拓扑排序dp
n个点m条边的有向图,每个点有一个权值,求一条路径,使路径经过的点权值之和最大。
思路:使用Tarjan缩点建立新图DAG,在DAG上进行拓扑排序并进行DP。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
| const int maxn=100005;
int tot=0,Index=0,cnt=0;
int stk[maxn],dfn[maxn],low[maxn],belong[maxn];
int val[maxn],rec[maxn];
bool vis[maxn];
vector<int> G[maxn];
void tarjan(int x)
{
dfn[x]=low[x]=++tim;
stk[++Index]=x;
vis[x]=1;
for(int &v:G[x])
{
if(!dfn[v])
{
tarjan(v);
low[x]=min(low[x],low[v]);
}
else if(vis[v])
low[x]=min(low[x],dfn[v]);
}
if(low[x]==dfn[x])
{
cnt++;
do{
belong[stk[Index]]=cnt;
rec[cnt]+=val[stk[Index]];
vis[stk[Index]]=0;
Index--;
}while(stk[Index+1]!=x);
}
}
vector<int> Gra[maxn];
int dp[maxn],top[maxn],into[maxn];
int topsort(void)
{
queue<int> QAQ;
for(int i=1;i<=cnt;i++)
{
if(!into[i])
QAQ.push(i);
dp[i]=rec[i];
}
int flag=0;
while(!QAQ.empty())
{
int x=QAQ.front();
QAQ.pop();
top[x]=++flag;
for(int i=0;i<Gra[x].size();i++)
{
dp[Gra[x][i]]=max(dp[Gra[x][i]],dp[x]+rec[Gra[x][i]]);
if(--into[Gra[x][i]]==0)
QAQ.push(Gra[x][i]);
}
}
int ans=0;
for(int i=1;i<=cnt;i++)
ans=max(ans,dp[i]);
return ans;
}
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
cin>>val[i];
for(int i=0;i<m;i++)
{
int u,v;
cin>>u>>v;
G[u].push_back(v);
}
for(int i=1;i<=n;i++)
if(!dfn[i])
tarjan(i);
for(int i=1;i<=m;i++)
for(int j=0;j<G[i].size();j++)
{
int x=belong[i],y=belong[G[i][j]];
if(x!=y)
{
Gra[x].push_back(y);
into[y]++;
}
}
cout<<topsort()<<endl;
return 0;
}
|
双连通分量(biconnected component)
双连通分量概念: 双连通分量有点双连通分量和边双连通分量两种。若一个无向图中的去掉任意一个节点(一条边)都不会改变此图的连通性,即不存在割。
割点:去掉这个点,原无向联通图不再联通。
割边/桥:去掉这条边,原无向联通图不再联通。
点双连通:删掉一个点之后,图仍联通
边双连通:删掉一条边之后,图仍联通
点双连通:在一个无向图中,若任意两点间至少存在两条“点不重复”的路径,则说这个图是点双连通的。点双连通的极大子图称为点双连通分量(简称双连通分量,Biconnected Component,BCC)。
点双连通图不存在割点的图,边双连通图即不存在桥的图。
- BCC中无割点,任意两点间至少存在两条点不重复的路径等价于图中删去任意一个点都不会改变图的连通性
- 若BCC间有公共点,则公共点为原图的割点
- 无向连通图中割点一定属于至少两个BCC,非割点只属于一个BCC
点双连通分量缩点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| int dfn[maxn],low[maxn],stk[maxn],belong[maxn],index=0,cnt=0,tim=0;
vector<int>G[maxn],g[maxn];
bool vis[maxn];
void tarjan(int x,int fa)
{
low[x]=dfn[x]=++tim;
vis[x]=1;
stk[++index]=x;
for(int &v:G[x])
{
if(v==fa)
continue;
if(!vis[v])
{
tarjan(v,x);
low[x]=min(low[x],low[v]);
}
else
low[x]=min(low[x],dfn[v]);
}
if(low[x]==dfn[x]&&vis[x])
{
cnt++;
do{
belong[stk[index]]=cnt;
vis[stk[index]]=0;
index--;
}while(stk[index+1]!=x);
}
}
|
Tarjan无向图求割点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| int tot=0,Index=0,ans=0,cnt=0;
int dfn[maxn],low[maxn],stk[maxn];
bool vis[maxn],isc[maxn];
void tarjan(int x,int fa)
{
dfn[x]=low[x]=++tot;
int child=0;
for(int i=0;i<G[x].size();i++)
{
int v=G[x][i];
if(!dfn[v])
{
tarjan(v,x);
low[x]=min(low[x],low[v]);
if(x==fa)
child++;
if(x!=fa&&low[v]>=dfn[x])
isc[x]=1;
}
else if(v!=fa)
low[x]=min(low[x],dfn[v]);
}
if(x==fa&&child>=2)
isc[x]=1;
}
|
无向图求桥
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| void tarjan(int x,int fa)
{
dfn[x]=low[x]=++tot;
bool vis=0;
for(int i=0;i<G[x].size();i++)
{
int v=G[x][i].v,no=G[x][i].no;
if(!dfn[v])
{
tarjan(v,x);
if(low[v]>dfn[x])
{
bri[no]=1;
}
low[x]=min(low[x],low[v]);
}
else if(dfn[x]>dfn[v])
{
if(v==fa&&!vis)
vis=1;
else
low[x]=min(low[x],dfn[v]);
}
}
}
|
2-SAT问题
流程
- 将点$i$拆成$i$与$n+i$两个点,分别表示点$i$状态为$0$或$1$,二者必须且只能取其一。
- 根据所给逻辑关系建图,将$2n$个点进行缩点。
- 若存在一对拆点位于同一个强连通分量,则无解。
- 否则对于每个点对,选择分量编号较小的点(即拓扑序较大的那个)。
建图方式
| 逻辑表达式 |
连接的有向边(推导关系) |
| $a=1$,$a$单个点必为真,为假同理 |
$\lnot a \rightarrow a$ |
| $a\land b=1$ |
$\lnot a\rightarrow a,\lnot b \rightarrow b$ |
| $a\land b=0$ |
$a\rightarrow \lnot b,b \rightarrow \lnot a$ |
| $a \lor b=1$ |
$\lnot a\rightarrow b,\lnot b \rightarrow a$ |
| $a \lor b=0$ |
$a\rightarrow \lnot a,b \rightarrow \lnot b$ |
| $a\oplus b=1$ |
$\lnot a\rightarrow b,b \rightarrow \lnot a,\lnot b \rightarrow a,a\rightarrow \lnot b$ |
| $a\oplus b=0$,或$a\odot b=1$ |
$a\rightarrow b,b\rightarrow a,\lnot a\rightarrow \lnot b,\lnot b\rightarrow \lnot a$ |
| $a\rightarrow b$,$\lnot a \lor b$,为假当且仅当$a$为真$b$为假 |
$a\rightarrow b,\lnot b\rightarrow\lnot a$ |
| $\lnot a\rightarrow\lnot b,a\lor \lnot b$ |
$\lnot a\rightarrow\lnot b,b\rightarrow a$ |
圆方树
圆方树就是一种将图变成树的方法,可以处理仙人掌(每条边在不超过一个简单环中的无向图)。
顶点仙人掌:每个点不会在超过一个简单环中的联通无向图,其特点为缩点后每个点不会在超过两个BCC中。
在圆方树中,原来的每个点对应一个圆点,每一个点双对应一个方点。所以共有 $n+c$ 个点,其中 $n$ 是原图点数,$c$ 是原图点双连通分量的个数。如果原图有 $k$ 个连通分量,则它的圆方树也会形成 $k$ 棵树形成的森林。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| namespace rst{
int siz[maxn<<1],dfn[maxn],low[maxn],dfc=0,stk[maxn],top=0;
int belong[maxn<<1],cnt=0,n;
vector<int>pg[maxn],G[maxn<<1];
void tarjan(int x)
{
dfn[x]=low[x]=++dfc;
fprintf(stderr,"Enter: #%d,dfn=%d\n",x,dfn[x]);
stk[++top]=x;
for(auto &v:pg[x])
{
if(!dfn[v])
{
tarjan(v);
low[x]=std::min(low[x],low[v]);
if(low[v]==dfn[x])
{
cnt++;
fprintf(stderr,"\nFind a new bcc #%d.\n",cnt-n);
do{
G[cnt].push_back(stk[top]);
G[stk[top]].push_back(cnt);
siz[cnt]++;
fprintf(stderr,"Bcc #%d has vertex #%d.\n",cnt-n,stk[top]);
top--;
}while(stk[top+1]!=v);
siz[cnt]++;
G[cnt].push_back(x);
G[x].push_back(cnt);
fprintf(stderr,"Bcc #%d has top vertex #%d\nsize = %d.\n",cnt-n,x,siz[cnt]);
}
}
else
low[x]=std::min(low[x],dfn[v]);
}
fprintf(stderr,"");
}
void build(int n)
{
rst::n=cnt=n;
top=dfc=0;
for(int i=1;i<=n;i++)
if(!dfn[i])
tarjan(i),top--;
}
}
|
最近公共祖先(LCA)
因为LCA只适用于树,所以经常和生成树在一起考。
倍增
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| const int maxn=100005;
const int maxl=30;
vector<int> G[maxn];
int gene[maxn][maxl],depth[maxn],lg[maxn];
int nodes[maxn];
void dfs(int x,int fa)
{
depth[x]=depth[fa]+1;
gene[x][0]=fa;
nodes[x]=1;
for(int i=1;(1<<i)<=depth[x];i++)
gene[x][i]=gene[gene[x][i-1]][i-1];
for(int i=0;i<G[x].size();i++)
if(G[x][i]!=fa)
{
dfs(G[x][i],x);
nodes[x]+=nodes[G[x][i]];
}
}
int lca(int x,int y)
{
if(depth[x]<depth[y])
swap(x,y);
while(depth[x]>depth[y])
x=gene[x][lg[depth[x]-depth[y]-1]];
if(x==y)
return x;
for(int i=lg[depth[x]];i>=0;i--)
if(gene[x][i]!=gene[y][i])
{
x=gene[x][i];
y=gene[y][i];
}
return gene[x][0];
}
int dist(int x,int y)
{
int tem=lca(x,y);
return (int)(abs(depth[x]-depth[tem])+abs(depth[y]-depth[tem]));
}
void init(int s,int n)
{
memset(nodes,0,sizeof(nodes));
depth[s]=1;
for(int i=1;i<=n;i++)
lg[i]=lg[i-1]+((1<<(lg[i-1]+1))==i);
dfs(s,0);
}
|
应用
次小生成树:P4180严格次小生成树
树上两条路径是否相交:仓鼠找sugar
1
2
3
| u=lca(a,b),v=lca(c,d);
if(dist(u,c)+dist(u,d)==dist(c,d)||dist(v,a)+dist(v,b)==dist(a,b))
cout<<"Yes"<<endl;
|
给定节点,求以它为LCA的节点有多少种组合:找祖先 ,DFS回溯求出
分类讨论求树上到任意两点距离相等的点的个数(重点讨论中节点与LCA关系):A and B and Lecture Rooms
求两节点路径上最大/最小边的权值,若求最小即为求容量:货车运输 ,DFS时倍增求出路径上min
树上差分
用于求解一些树上路径问题。
常见问法:将一棵树上从u到v路径上的点/边的权值加上x,询问某点/边的权值。
$O(1)$修改,$O(n)$查询,复杂度决定要离线。
强行在线可用树链剖分$O(\log n \times \log n)$修改,$O( \log n \times \log n)$查询。
修改差分数组之前先用DFS倍增求出各节点LCA。
差分数组记为power[maxn],直接修改即可,查询时调用DFS
性质
- 树上任意两点之间有且只有一条路径
- 一个节点只有一个父节点
- $x$节点到$y$结点的路线为:$x→lca(x,y)→y$
点的差分
操作
每次修改使$u$到$v$的路径上所有节点权值+1(包括端点),询问某一节点权值。
修改
$power[u]++,\ power[v]++,\ power[lca(u,v)]–,\ power[father[lca(u,v)]]–$
边的差分
操作
以点代边,$power[x]$代表$x$节点到父节点的边的权值。
若查询边的权值,则需要按输入顺序对每条边进行编号。
每次修改使节点$u$与节点$v$之间所有边权值+1,询问某一条边权值。
修改
$power[u]++,\ power[v]++,\ power[lca(u,v)]-=2$
查询
1
2
3
4
5
6
7
8
9
10
11
| int power[maxn];
void dfs(int x)
{
for(int i=head[x];~i;i=G[i].nex)
if(G[i].v!=gene[x][0])
{
dfs(G[i].v);
power[x]+=power[G[i].v];
}
ans=max(ans,power[x]);
}
|
树链剖分
注意以点代边的思想
- 功能
- 更新/查询某个节点子树的权值
- 更新/查询树上两个节点间所有点的权值
- 性质
- 子树的时间戳一定全部小于父节点,并且连续(所以可用线段树维护)
- 任何一条路径都是由重链的一部分与重链间的叶子节点构成
- 任何父节点都一定在一条重链上(所以可用top的父节点跳链)
- 例题
- P3384 树链剖分
通用模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
| int n,tot=0,head[maxn];
double val[maxn];
struct edge
{
int v,nex;
ll w;
} e[maxn<<1];
inline void add(int u,int v,ll w=0)
{
e[++tot].v=v;
e[tot].w=w;
e[tot].nex=head[u];
head[u]=tot;
}
namespace hld{
int n,father[maxn],son[maxn],depth[maxn],siz[maxn];
int tim=0,dfn[maxn],rk[maxn],top[maxn];
using type=long long;
type w[maxn];
void init(int N)
{
n=N;
tim=tot=0;
memset(head,-1,sizeof(head));
memset(depth,0,sizeof(depth));
memset(son,0,sizeof(son));
memset(dfn,0,sizeof(dfn));
}
void dfs1(int x,int fa)
{
depth[x]=depth[fa]+1;
father[x]=fa;
siz[x]=1;
int maxsiz=-1;
for(int i=head[x];~i;i=e[i].nex)
{
int v=e[i].v;
if(v==fa)
continue;
dfs1(v,x);
siz[x]+=siz[v];
if(maxsiz<siz[v])
{
son[x]=v;
maxsiz=siz[v];
}
}
}
void dfs2(int x,int t)
{
dfn[x]=++tim;
rk[tim]=x;
top[x]=t;
w[tim]=val[x];
if(!son[x])
return;
dfs2(son[x],t);
for(int i=head[x];~i;i=e[i].nex)
if(e[i].v!=father[x]&&e[i].v!=son[x])
dfs2(e[i].v,e[i].v);
}
int lca(int x,int y)
{
while(top[x]!=top[y])
{
if(depth[top[x]]<depth[top[y]])
swap(x,y);
x=father[top[x]];
}
return (depth[x]>depth[y])?y:x;
}
struct node
{
type val,Max,lazy;
} tree[maxn<<2];
inline void pushup(int root)
{
tree[root].val=tree[root<<1].val+tree[root<<1|1].val;
tree[root].Max=max(tree[root<<1].Max,tree[root<<1|1].Max);
}
void build(int root=1,int l=1,int r=n)
{
tree[root].lazy=0;
if(l==r)
tree[root].val=tree[root].Max=w[l];
else{
int mid=(l+r)>>1;
build(root<<1,l,mid);
build(root<<1|1,mid+1,r);
pushup(root);
}
}
inline void pushdown(int root,int l,int r)
{
if(tree[root].lazy)
{
int mid=(l+r)>>1;
tree[root<<1].val=tree[root<<1].val+tree[root].lazy*(mid-l+1);
tree[root<<1|1].val=tree[root<<1|1].val+tree[root].lazy*(r-mid);
tree[root<<1].Max+=tree[root].lazy;
tree[root<<1|1].Max+=tree[root].lazy;
tree[root<<1].lazy+=tree[root].lazy;
tree[root<<1|1].lazy+=tree[root].lazy;
tree[root].lazy=0;
}
}
void modify(int root,int nst,int ned,int ust,int ued,type num)
{
if(ned<ust||ued<nst)
return;
if(ust<=nst&&ued>=ned)
{
tree[root].val=tree[root].val+(ned-nst+1)*num;
tree[root].Max+=num;
tree[root].lazy+=num;
return;
}
pushdown(root,nst,ned);
int mid=(nst+ned)>>1;
modify(root<<1,nst,mid,ust,ued,num);
modify(root<<1|1,mid+1,ned,ust,ued,num);
pushup(root);
}
type query(int root,int nst,int ned,int qst,int qed)
{
if(ned<qst||qed<nst)
return 0;
if(qst<=nst&&ned<=qed)
return tree[root].val;
pushdown(root,nst,ned);
int mid=(nst+ned)>>1;
return query(root<<1,nst,mid,qst,qed)+query(root<<1|1,mid+1,ned,qst,qed);
}
type qmax(int root,int nst,int ned,int qst,int qed)
{
if(ned<qst||qed<nst)
return LLONG_MIN;
if(qst<=nst&&ned<=qed)
return tree[root].Max;
pushdown(root,nst,ned);
int mid=(nst+ned)>>1;
return max(qmax(root<<1,nst,mid,qst,qed),qmax(root<<1|1,mid+1,ned,qst,qed));
}
inline void mson(int x,type addnum,int n=n)
{
modify(1,1,n,dfn[x],dfn[x]+siz[x]-1,addnum);
}
inline type sonsum(int x,int n=n)
{
return query(1,1,n,dfn[x],dfn[x]+siz[x]-1);
}
type sonmax(int x,int n=n)
{
return qmax(1,1,n,dfn[x],dfn[x]+siz[x]-1);
}
void mchain(int x,int y,type addnum,int n=n)
{
while(top[x]!=top[y])
{
if(depth[top[x]]<depth[top[y]])
swap(x,y);
modify(1,1,n,dfn[top[x]],dfn[x],addnum);
x=father[top[x]];
}
if(depth[x]>depth[y])
swap(x,y);
modify(1,1,n,dfn[x],dfn[y],addnum);
}
type chainsum(int x,int y,int n=n)
{
type ret=0;
while(top[x]!=top[y])
{
if(depth[top[x]]<depth[top[y]])
swap(x,y);
ret+=query(1,1,n,dfn[top[x]],dfn[x]);
x=father[top[x]];
}
if(depth[x]>depth[y])
swap(x,y);
return ret+query(1,1,n,dfn[x],dfn[y]);
}
type chainmax(int x,int y,int n=n)
{
type ret=LLONG_MIN;
while(top[x]!=top[y])
{
if(depth[top[x]]<depth[top[y]])
swap(x,y);
ret=max(ret,qmax(1,1,n,dfn[top[x]],dfn[x]));
x=father[top[x]];
}
if(depth[x]>depth[y])
swap(x,y);
return max(ret,qmax(1,1,n,dfn[x],dfn[y]));
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
| #include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int inf=0x3f3f3f3f;
const int maxn=100005;
int mod=100000007;
int head[maxn],cnt=0;
struct edge
{
int v,nex;
} e[maxn<<1];
int father[maxn],son[maxn];
int depth[maxn],siz[maxn],top[maxn];
int tim=0,dfn[maxn],rk[maxn],w[maxn];
int val[maxn];
void add(int u,int v)
{
e[++cnt].v=v;
e[cnt].nex=head[u];
head[u]=cnt;
}
void dfs1(int x,int fa)
{
father[x]=fa;
depth[x]=depth[fa]+1;
siz[x]=1;
int maxsize=-1;
for(int i=head[x];~i;i=e[i].nex)
{
int v=e[i].v;
if(v==fa)
continue;
dfs1(v,x);
siz[x]+=siz[v];
if(siz[v]>maxsize)
{
maxsize=siz[v];
son[x]=v;
}
}
}
void dfs2(int x,int t)
{
top[x]=t;
dfn[x]=++tim;
rk[tim]=x;
w[tim]=val[x];
if(!son[x])
return;
dfs2(son[x],t);
for(int i=head[x];~i;i=e[i].nex)
{
if(e[i].v!=son[x]&&e[i].v!=father[x])
dfs2(e[i].v,e[i].v);
}
}
struct node
{
int val,lazy;
} tree[maxn<<2];
inline void pushup(int root)
{
tree[root].val=(tree[root<<1].val+tree[root<<1|1].val)%mod;
}
void build(int root,int l,int r)
{
tree[root].val=tree[root].lazy=0;
if(l==r)
tree[root].val=w[l]%mod;
else{
int mid=(l+r)>>1;
build(root<<1,l,mid);
build(root<<1|1,mid+1,r);
pushup(root);
}
}
inline void pushdown(int root,int l,int r)
{
if(tree[root].lazy)
{
int mid=(l+r)>>1;
tree[root<<1].val=(tree[root<<1].val%mod+(tree[root].lazy%mod*(mid-l+1))%mod)%mod;
tree[root<<1|1].val=(tree[root<<1|1].val%mod+(tree[root].lazy%mod*(r-mid)%mod))%mod;
tree[root<<1].lazy=(tree[root<<1].lazy%mod+tree[root].lazy%mod)%mod;
tree[root<<1|1].lazy=(tree[root<<1|1].lazy%mod+tree[root].lazy%mod)%mod;
tree[root].lazy=0;
}
}
void modify(int root,int nst,int ned,int ust,int ued,int num)
{
if(ned<ust||ued<nst)
return;
if(ust<=nst&&ued>=ned)
{
tree[root].lazy=(tree[root].lazy%mod+num%mod)%mod;
tree[root].val=(tree[root].val%mod+((ned-nst+1)%mod*(num%mod))%mod)%mod;
return;
}
pushdown(root,nst,ned);
int mid=(nst+ned)>>1;
modify(root<<1,nst,mid,ust,ued,num);
modify(root<<1|1,mid+1,ned,ust,ued,num);
pushup(root);
}
int query(int root,int nst,int ned,int qst,int qed)
{
if(ned<qst||qed<nst)
return 0;
if(qst<=nst&&qed>=ned)
{
return tree[root].val%mod;
}
pushdown(root,nst,ned);
int mid=(nst+ned)>>1;
return (query(root<<1,nst,mid,qst,qed)+query(root<<1|1,mid+1,ned,qst,qed))%mod;
}
inline void mson(int x,int n,int addnum)
{
modify(1,1,n,dfn[x],dfn[x]+siz[x]-1,addnum);
}
inline int qson(int x,int n)
{
return query(1,1,n,dfn[x],dfn[x]+siz[x]-1)%mod;
}
void mchain(int x,int y,int n,int addnum)
{
addnum%=mod;
while(top[x]!=top[y])
{
if(depth[top[x]]<depth[top[y]])
swap(x,y);
modify(1,1,n,dfn[top[x]],dfn[x],addnum);
x=father[top[x]];
}
if(depth[x]>depth[y])
swap(x,y);
modify(1,1,n,dfn[x],dfn[y],addnum);
}
int qchain(int x,int y,int n)
{
int ret=0;
while(top[x]!=top[y])
{
if(depth[top[x]]<depth[top[y]])
swap(x,y);
ret=(ret+query(1,1,n,dfn[top[x]],dfn[x]))%mod;
x=father[top[x]];
}
if(depth[x]>depth[y])
swap(x,y);
return (ret+query(1,1,n,dfn[x],dfn[y]))%mod;
}
int main()
{
int n,m,p,r;
scanf("%d%d%d%d",&n,&m,&r,&mod);
memset(head,-1,sizeof(head));
for(int i=1;i<=n;i++)
scanf("%d",&val[i]);
for(int i=1;i<n;i++)
{
int u,v;
scanf("%d%d",&u,&v);
add(u,v);
add(v,u);
}
dfs1(r,r);
dfs2(r,r);
build(1,1,n);
while(m--)
{
int ope,x,y,z;
scanf("%d",&ope);
if(ope==1)
{
scanf("%d%d%d",&x,&y,&z);
mchain(x,y,n,z);
}
else if(ope==2)
{
scanf("%d%d",&x,&y);
printf("%d\n",qchain(x,y,n));
}
else if(ope==3)
{
scanf("%d%d",&x,&z);
mson(x,n,z);
}
else{
scanf("%d",&x);
printf("%d\n",qson(x,n));
}
}
return 0;
}
|
点分治
树的重心
- 也叫树的质心。找到一个点,其所有的子树中最大的子树节点数最少,那么这个点就是这棵树的重心,删去重心后,生成的多棵树尽可能平衡。
流程
- 找出当前树的重心
- 因为分治步骤二需要将sum赋值为当前树大小(siz[v]),所以getrt要跑两遍
- 处理经过中心的路径
- 删除树的重心
- 对新得到的子树重复上述步骤
例题
一棵n节点的树,询问树上距离为k的点对是否存在。离线操作。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
| #include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=10005;
const int maxk=10000005;
int tot=0,head[maxn];
struct edge
{
int v,nex,w;
} e[maxn<<1];
inline void add(int u,int v,ll w)
{
e[++tot].v=v;
e[tot].nex=head[u];
e[tot].w=w;
head[u]=tot;
}
int n,m,root,sum=0;
int siz[maxn],maxp[maxn];
bool vis[maxn];
void getrt(int x,int fa)
{
siz[x]=1,maxp[x]=0;
for(int i=head[x];~i;i=e[i].nex)
{
int v=e[i].v;
if(v==fa||vis[v])
continue;
getrt(v,x);
siz[x]+=siz[v];
if(siz[v]>maxp[x])
maxp[x]=siz[v];
}
maxp[x]=max(maxp[x],sum-siz[x]);
if(maxp[x]<maxp[root])
root=x;
}
int dist[maxn],tmp[maxn],cnt=0;
void getdist(int x,int fa)
{
tmp[++cnt]=dist[x];
for(int i=head[x];~i;i=e[i].nex)
{
int v=e[i].v;
if(v==fa||vis[v])
continue;
dist[v]=dist[x]+e[i].w;
getdist(v,x);
}
}
int q[105];
bool jud[maxk],ans[105];
queue<int> QwQ;
void solve(int x)
{
for(int i=head[x];~i;i=e[i].nex)
{
int v=e[i].v;
if(vis[v])
continue;
cnt=0;
dist[v]=e[i].w;
getdist(v,x);
for(int j=1;j<=cnt;j++)
for(int k=1;k<=m;k++)
if(q[k]>=tmp[j])
ans[k]|=jud[q[k]-tmp[j]];
for(int j=1;j<=cnt;j++)
{
QwQ.push(tmp[j]);
jud[tmp[j]]=1;
}
}
while(!QwQ.empty())
{
jud[QwQ.front()]=0;
QwQ.pop();
}
}
void divide(int x)
{
vis[x]=jud[0]=1;
solve(x);
for(int i=head[x];~i;i=e[i].nex)
{
int v=e[i].v;
if(vis[v])
continue;
maxp[root=0]=sum=siz[v];
getrt(v,0);
getrt(root,0);
divide(root);
}
}
int main()
{
int k,u,v;
ll w;
memset(head,-1,sizeof(head));
cin>>n>>m;
for(int i=1;i<n;i++)
{
cin>>u>>v>>w;
add(u,v,w);
add(v,u,w);
}
for(int i=1;i<=m;i++)
cin>>q[i];
maxp[0]=sum=n;
getrt(1,0);
getrt(root,0);
divide(root);
for(int i=1;i<=m;i++)
cout<<(ans[i]?"AYE":"NAY")<<'\n';
return 0;
}
|
树上启发式合并(DSU on tree)
解决离线子树查询问题,即统计树上一个节点的子树中具有某种特征的节点数。
一般也可以使用DFS序莫队或DFS序主席树做。
时间复杂度$O(nlogn)$,空间复杂度$O(n)$。
流程
- 先用dfs处理出重儿子
- 使用DFS处理各子树信息,设当前子树根节点为x
- 遍历x的轻儿子,计算轻儿子子树贡献,记录到ans数组,信息不做保留。
- 处理x的重儿子子树贡献,记录到ans数组,并保留。
- 暴力统计节点x及所有轻儿子子树贡献,与x的重儿子子树贡献汇总,一同回溯到上一级,以便处理出以x节点的父节点为根的子树的贡献。
例题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
| #include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=100005;
int head[maxn],tot;
struct Edge
{
int v,nex;
} e[maxn<<1];
inline void add(int u,int v)
{
e[++tot].v=v;
e[tot].nex=head[u];
head[u]=tot;
}
int siz[maxn],son[maxn];
void dfs(int x,int fa)
{
siz[x]=1;
for(int i=head[x];~i;i=e[i].nex)
{
int v=e[i].v;
if(v==fa)
continue;
dfs(v,x);
siz[x]+=siz[v];
if(siz[v]>siz[son[x]])
son[x]=v;
}
}
int color[maxn],cnt[maxn];
ll ans[maxn],sum;
int flag,maxc;
void cal(int x,int fa,int val)
{
cnt[color[x]]+=val;
if(cnt[color[x]]>maxc)
{
sum=color[x];
maxc=cnt[color[x]];
}
else if(cnt[color[x]]==maxc)
sum+=color[x];
for(int i=head[x];~i;i=e[i].nex)
{
int v=e[i].v;
if(v==fa||v==flag)
continue;
cal(v,x,val);
}
}
void dfs(int x,int fa,bool keep)
{
for(int i=head[x];~i;i=e[i].nex)
{
int v=e[i].v;
if(v==fa||v==son[x])
continue;
dfs(v,x,0);
}
if(son[x])
{
dfs(son[x],x,1);
flag=son[x];
}
cal(x,fa,1);
ans[x]=sum;
flag=0;
if(!keep)
{
memset(cnt,0,sizeof(cnt));
sum=maxc=0;
}
}
int main()
{
memset(head,-1,sizeof(head));
int n;
cin>>n;
for(int i=1;i<=n;i++)
cin>>color[i];
for(int i=1;i<n;i++)
{
int u,v;
cin>>u>>v;
add(u,v);
add(v,u);
}
dfs(1,0);
dfs(1,0,0);
for(int i=1;i<=n;i++)
cout<<ans[i]<<' ';
return 0;
}
|
二分图
二分图如果不考虑复杂度的话,可以用网络流来做。
定义
- 最大匹配:二分图中边集的数目最大的匹配。
- 匹配:子图$M$上任意两条边都不依附于同一个顶点,则称$M$为原图的匹配。
- 点覆盖:图$G=(V,E)$中的一个点覆盖为一个集合$S⊆V$使得每条边至少有一个端点在$S$中。
- 最小点覆盖:点个数最少的$S$集合。
- 最小边覆盖:用最少不相交简单路径覆盖DAG所有顶点。
- 最小点权覆盖:覆盖每个节点都需要一定代价,覆盖所有边总代价最小的点集。
- 最大独立集:在点集$V$中选出$M$个点,$M$中点与点两两无边,并使$M$最大。
常见二分图结论
- 最小点覆盖=二分图最大匹配
- 最小边覆盖=顶点数-最小顶点覆盖(二分图最大匹配)
- 最大独立集=顶点数-最大匹配数
- 所有回路长度均为偶数
适用任意图的结论
二分图判定(黑白染色法)
A、B集合分别染成不同颜色(由边链接的两节点颜色一定不同)
A集合中选取一个起始节点,将邻接的点染成与其不同的颜色,如果邻接的点有相同颜色的,则说明不是二分图
匈牙利算法
邻接表
时间复杂度O(nm),有重边时使用邻接矩阵?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| const int maxn=205;
vector<int> G[maxn];
int linker[maxn];
bool used[maxn];
bool dfs(int x)
{
for(auto &v:G[x])
if(!used[v])
{
used[v]=1;
if(!linker[v]||dfs(linker[v]))
{
linker[v]=x;
return 1;
}
}
return 0;
}
int hungry(int n)
{
int ans=0;
memset(linker,0,sizeof(linker));
for(int i=1;i<=n;i++)
{
memset(used,0,sizeof(used));
if(dfs(i))
ans++;
}
return ans;
}
|
KM算法
- 二分图最佳完美匹配:带权二分图,求一种完备匹配方案,使得所有匹配边的权和最大。
BFS,复杂度稳的一批
复杂度$O(n^3)$,使用时清空w数组,并且按照关系为w赋值,调用KM(n)即可得到匹配边权值和。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
| const int maxn=1005;
int w[maxn][maxn];
int lx[maxn],ly[maxn];
int linker[maxn];
int slack[maxn];
bool visy[maxn];
int pre[maxn];
void bfs(int k,int n)
{
int x,y=0,yy=0,delta;
memset(pre,0,sizeof(pre));
for(int i=1;i<=n;i++)
slack[i]=INF;
linker[y]=k;
while(1)
{
x=linker[y];
delta=INF;
visy[y]=true;
for(int i=1;i<=n;i++)
{
if(!visy[i])
{
if(slack[i]>lx[x]+ly[i]-w[x][i])
{
slack[i]=lx[x]+ly[i]-w[x][i];
pre[i]=y;
}
if(slack[i]<delta)
delta=slack[i],yy=i;
}
}
for(int i=0;i<=n;i++)
{
if( visy[i] )
lx[linker[i]]-=delta,ly[i]+=delta;
else
slack[i]-=delta;
}
y=yy;
if(linker[y]==-1)
break;
}
while(y)
linker[y]=linker[pre[y]],y=pre[y];
}
int KM(int n)
{
memset(lx,0,sizeof(lx));
memset(ly,0,sizeof(ly));
memset(linker,-1,sizeof(linker));
for(int i=1;i<=n;i++)
{
memset(visy,false,sizeof(visy));
bfs(i,n);
}
int ans=0;
for(int i=1;i<=n;i++)
{
if(linker[i]!=-1)
ans+=w[linker[i]][i];
}
return ans;
}
|
左右数目不等的模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| int wx[maxn],wy[maxn],match[maxn];
int mp[maxn][maxn],slack[maxn],pre[maxn];
bool viy[maxn];
void bfs(int k,int n,int m)
{
int py=0,px,yy=0,delta;
match[py]=k;
for(int i=0;i<=n;i++)pre[i]=0,slack[i]=inf;
do
{
px=match[py],delta=inf,viy[py]=1;
for(int i=1;i<=n;i++)
{
if(!viy[i])
{
if(wx[px]+wy[i]-mp[px][i]<slack[i])slack[i]=wx[px]+wy[i]-mp[px][i],pre[i]=py;
if(slack[i]<delta)delta=slack[i],yy=i;
}
}
for(int i=0;i<=n;i++)
{
if(viy[i])wx[match[i]]-=delta,wy[i]+=delta;
else slack[i]-=delta;
}
py=yy;
}while(match[py]!=0);
while(py)match[py]=match[pre[py]],py=pre[py];
}
int km(int n,int m)
{
for(int i=1;i<=n;i++)
wy[i]=0,match[i]=0;
for(int i=1;i<=m;i++)
{
wx[i]=0;
for(int j=1;j<=n;j++)
wx[i]=max(wx[i],mp[i][j]);
}
for(int i=1;i<=m;++i)
memset(viy,0,sizeof(viy)),bfs(i,n,m);
int ans=0;
for(int i=1;i<=n;++i)
ans+=wx[match[i]]+wy[i];
return ans;
}
|
CSL的写法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
| const int maxn = 305;
const int INF=0x3f3f3f3f;
int cost[maxn][maxn];
int lx[maxn], ly[maxn];
int match[maxn], slack[maxn];
int previous[maxn];
bool vy[maxn];
void augment(int root,int n)
{
fill(vy + 1, vy + n + 1, false);
fill(slack + 1, slack + n + 1, INF);
int py;
match[py = 0] = root;
do
{
vy[py] = true;
int x = match[py], yy;
int delta = INF;
for (int y = 1; y <= n; y++)
{
if (!vy[y])
{
if (lx[x] + ly[y] - cost[x][y] < slack[y])
slack[y] = lx[x] + ly[y] - cost[x][y], previous[y] = py;
if (slack[y] < delta)
delta = slack[y], yy = y;
}
}
for (int y = 0; y <= n; y++)
{
if (vy[y])
lx[match[y]] -= delta, ly[y] += delta;
else
slack[y] -= delta;
}
py = yy;
}
while(match[py] != -1);
do
{
int pre = previous[py];
match[py] = match[pre], py = pre;
} while (py);
}
int KM(int n)
{
for (int i = 1; i <= n; i++)
{
lx[i] = ly[i] = 0;
match[i] = -1;
for (int j = 1; j <= n; j++)
lx[i] = max(lx[i], cost[i][j]);
}
int answer = 0;
for (int root = 1; root <= n; root++)
augment(root,n);
for (int i = 1; i <= n; i++)
answer += lx[i], answer += ly[i];
return answer;
}
|
网络流
注意反向思考,添加新节点进行限流。
最小点覆盖=最大匹配 (与最大流最小割定理等价)。
最大独立集=点数-最大匹配 (独立集为点覆盖的补集)。
最小边覆盖=最大独立集 (独立集中每个点需要一条边去覆盖)。
最大独立集
方格取数问题
二分图最大独立集=顶点数-最大匹配数=点数-最小割
如果是点有点权,要求集合内两两无冲的情况下求集合最大价值。那么建立二分图,超级源点$s$和超级汇点$t$,因为图必须是二分图,分成黑点和白点两部分,黑点中与白点有关系,则连接一条容量为$inf$的边,黑点向$s$连一条容量为点价值的边,同样白点向$t$连一条容量为点价值的边。跑最大流求得最小割。
最大权闭合子图
定义有向图$G=(V,E)$的一个闭合子图是该有向图的一个点集,其中这个点集中的所有点的出边连向的还是点集中的点。
解法
加入超级源点$S$和超级汇点$T$,构造网络$G=(V,E)$:
- $S$与所有正权点连边,容量为正权点权值。
- 负权点向$T$连边,容量为负权点的绝对值。
- 0权点无影响可以任意当作正权点或负权点。
- 原图中的边保持不变,容量为$INF$。
原图对应的最大权闭合图的权值和为所有正权点的权值和减去最小割。
最大密度子图
定义一个无向图$G=(V,E)$的密度$D$为边数$|E|$和点数$|V|$的比值,即$D = \dfrac{|E|}{|V|}$.
最大密度子图$G’$即为无向图$G$的一个子图且具有最大的$D$.
解法1.二分,复杂度$logn.maxflow(n+m,n+m)$
二分答案$g$,下界为$\dfrac{1}{n}$,上界为$\dfrac{m}{1}$.
构造一个函数$h(g)=max(|E’|-g|V’|)$,子图.
设最优密度为$D$,当$h(g)=0$时$g$即为答案.
$$
\begin{cases}
h(g)<0 & g>D\
h(g)=0 & g=D\
h(g)>0 & g<D
\end{cases}
$$
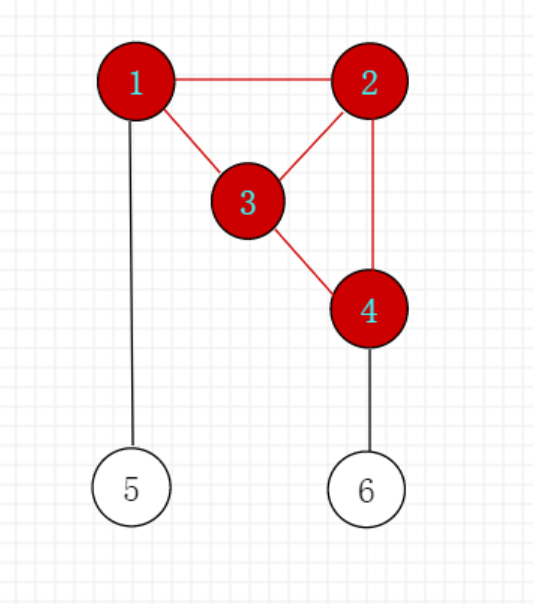
对于每条边$e<u,v> \in E$,加入子图的前提是$u,v$都在子图中,所以这部分可用最大闭合子图解决:
- 每条边$e$作为一个点,$e$向这条边的两个端点$u,v$连$INF$的边.
- s向所有原图中的边连边,容量为$1$.
- 原图中的点向t连边,容量为$g$.
.png)
搜索残余网络中源点可以到达的点即可得到子图中的点。
抱歉这题我写疯了过不去,贴了别人的代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
|
using namespace std;
const int maxn = 116;
const double INF = 0x3fffffff;
const double eps = 1e-8;
struct Edge
{
int to, rev;
double cap;
Edge(int to_, int rev_, double cap_):to(to_),rev(rev_),cap(cap_){}
};
vector<Edge> G[maxn];
vector<int> ans;
int level[maxn], n, m, s, t;
int iter[maxn], sum;
struct node
{
int first, second;
} p[1024];
bool vis[maxn];
int d[maxn];
void add_edge(int from, int to, double cap)
{
G[from].push_back(Edge(to, G[to].size(), cap));
G[to].push_back(Edge(from, G[from].size() - 1, 0.0));
}
void bfs(int s)
{
memset(level, -1, sizeof(level));
queue<int> q;
level[s] = 0;
q.push(s);
while(!q.empty()) {
int v = q.front(); q.pop();
for(int i = 0; i < G[v].size(); i++) {
Edge& e = G[v][i];
if(e.cap > eps && level[e.to] < 0) {
level[e.to] = level[v] + 1;
q.push(e.to);
}
}
}
}
double min(double a, double b)
{
return a > b ? b : a;
}
double dfs(int v, int t, double f)
{
if(v == t) return f;
for(int& i = iter[v]; i < G[v].size(); i++) {
Edge& e = G[v][i];
if(e.cap > 0 && level[e.to] > level[v]) {
double dt = dfs(e.to, t, min(f, e.cap));
if(dt > eps) {
e.cap -= dt;
G[e.to][e.rev].cap += dt;
return dt;
}
}
}
return 0;
}
double max_flow(int s, int t)
{
double flow = 0;
for(;;) {
bfs(s);
if(level[t] < 0) return flow;
memset(iter, 0, sizeof(iter));
double f;
while((f = dfs(s, t, INF)) > eps)
flow += f;
}
}
bool check(double k)
{
for(int i = 0; i < maxn; i++) G[i].clear();
for(int i = 1; i <= n; i++) {
add_edge(s, i, m);
add_edge(i, t, m + 2 * k - d[i]);
}
for(int i = 0; i < m; i++) {
int u = p[i].first, v = p[i].second;
add_edge(u, v, 1.0);
add_edge(v, u, 1.0);
}
double tmp = (n * m - max_flow(s, t)) / 2;
if(tmp > eps) return true;
else return false;
}
void dfs1(int v)
{
vis[v] = true;
for(int i = 0; i < G[v].size(); i++) {
Edge e = G[v][i];
if(e.cap > eps && !vis[e.to])
dfs1(e.to);
}
}
int main()
{
while(~scanf("%d%d", &n, &m)) {
memset(d, 0, sizeof(d));
for(int i = 0; i < m; i++) {
scanf("%d%d", &p[i].first, &p[i].second);
d[p[i].first]++;
d[p[i].second]++;
}
if(m == 0) {
printf("1\n1\n");
} else {
s = 0; t = n + 1;
double lb = 0.0, ub = m * 1.0, mid;
double precision = (double)(1.0 / n / n);
while(ub - lb >= precision) {
mid = (lb + ub) / 2;
if(check(mid)) lb = mid;
else ub = mid;
}
check(lb);
memset(vis, 0, sizeof(vis));
dfs1(0);
sum = 0;
for(int i = 1; i <= n; i++)
if(vis[i]) sum++;
printf("%d\n", sum);
for(int i = 1; i <= n; i++)
if(vis[i]) printf("%d\n", i);
}
}
return 0;
}
|
以及下面这个,我和他写的一样
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
| #include<iostream>
#include<cstring>
#include<cmath>
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=40018,inf=1e9;
struct edg{
int nxt,to;
double f;
}e[maxn];
int cnt,vis[maxn],head,tail,q[maxn],S,T,n,m,t,last[maxn],d[maxn];
double l,r,mid;
void add(int x,int y,double z){
++t;e[t].nxt=last[x];last[x]=t;e[t].to=y;e[t].f=z;
++t;e[t].nxt=last[y];last[y]=t;e[t].to=x;e[t].f=0;
}
struct dui{
int from,to;
}qq[maxn];
int bfs(){
head=tail=0;
memset(d,-1,sizeof(d));
q[++tail]=S;d[S]=0;
while(head<tail){
int u=q[++head];
for(int i=last[u];i;i=e[i].nxt){
int v=e[i].to;
if(e[i].f&&d[v]==-1){
d[v]=d[u]+1;
q[++tail]=v;
}
}
}
return d[T]!=-1;
}
double dfs(int x,double h){
if(x==T){return h;}
double tmp=0,cp;
for(int i=last[x];i;i=e[i].nxt){
int v=e[i].to;
if(e[i].f&&d[v]==d[x]+1){
cp=dfs(v,min(h-tmp,e[i].f));
e[i].f-=cp;e[i^1].f+=cp;tmp+=cp;
if(tmp==h){return tmp;}
}
}
if(!tmp)d[x]=-2;
return tmp;
}
int pd(double mid){
memset(last,0,sizeof(last));t=1;
for(int i=1;i<=m;++i){
add(n+i,qq[i].from,inf);
add(n+i,qq[i].to,inf);
add(S,n+i,1.0);
}
for(int i=1;i<=n;++i){
add(i,T,mid);
}
double pp,res=0;
while(bfs()){
while(pp=dfs(S,inf))res+=pp;
}
return (double(m)-res)>0;
}
void dfs1(int x){
vis[x]=1;
if(x>=1&&x<=n)cnt++;
for(int i=last[x];i;i=e[i].nxt){
int v=e[i].to;
if(e[i].f&&!vis[v])dfs1(v);
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=m;++i){
scanf("%d%d",&qq[i].from,&qq[i].to);
}
if(!m){puts("1");puts("1");return 0;}
l=0,r=m+1;S=n+m+1,T=n+m+2;
while(r-l>=1.0/n/n){
mid=(l+r)/2;
if(pd(mid))l=mid;
else r=mid;
}
pd(l);
dfs1(S);
printf("%d\n",cnt);
for(int i=1;i<=n;++i){
if(vis[i])
printf("%d\n",i);
}
return 0;
}
|
模板部分
dinic
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
| struct Dinic
{
struct Edge
{
int from, to, cap, flow;
Edge(int u, int v, int c, int f):
from(u), to(v), cap(c), flow(f) {}
};
int n, m, s, t;
vector<Edge> edges;
vector<int> G[maxn];
bool vis[maxn];
int d[maxn];
int cur[maxn];
void init(int n)
{
this->n = n;
for (int i = 0; i < n; i++) G[i].clear();
edges.clear();
}
void AddEdge(int from, int to, int cap)
{
edges.push_back(Edge(from, to, cap, 0));
edges.push_back(Edge(to, from, 0, 0));
m = edges.size();
G[from].push_back(m - 2);
G[to].push_back(m - 1);
}
bool BFS()
{
memset(vis, 0, sizeof(vis));
queue<int> q;
q.push(s);
d[s] = 0;
vis[s] = 1;
while (!q.empty())
{
int x = q.front();
q.pop();
for (int i = 0; i < G[x].size(); i++)
{
Edge& e = edges[G[x][i]];
if (!vis[e.to] && e.cap > e.flow)
{
vis[e.to] = 1;
d[e.to] = d[x] + 1;
q.push(e.to);
}
}
}
return vis[t];
}
int DFS(int x, int a)
{
if(x==t||a==0)
return a;
int flow = 0, f;
for(int& i=cur[x];i<G[x].size();i++)
{
Edge& e = edges[G[x][i]];
if(d[x]+1==d[e.to]&&(f=DFS(e.to,min(a,e.cap-e.flow))) > 0)
{
e.flow += f;
edges[G[x][i]^1].flow -= f;
flow += f;
a -= f;
if(a==0)
break;
}
}
if(!flow)
d[x] = -1;
return flow;
}
int Maxflow(int s, int t)
{
this->s = s, this->t = t;
int flow = 0;
while (BFS())
{
memset(cur, 0, sizeof(cur));
flow += DFS(s,inf);
}
return flow;
}
} di;
|
dijkstra费用流
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
| struct MCMF {
using type = ll;
struct Edge {
ll v, cap;
type cost;
ll rev;
};
const type INF=0x3f3f3f3f3f3f3f3f;
ll flow, s, t, n;
type cost;
type dist[maxn], H[maxn];
ll pv[maxn], pe[maxn];
std::vector<Edge> G[maxn];
void init(int n){
this->n = n;
for (int i = 0; i <= n; ++i) G[i].clear();
}
void addEdge(int u, int v, int cap, type cost){
G[u].push_back({v,cap,cost,G[v].size()});
G[v].push_back({u,0,-cost,G[u].size()-1});
}
bool dijkstra()
{
std::priority_queue<pair<type,ll>, std::vector<pair<type,ll>>, std::greater<pair<type,ll>> > q;
std::fill(dist, dist + n + 1, INF);
dist[s] = 0; q.push({ 0, s });
while (!q.empty())
{
pair<type,ll> x = q.top(); q.pop();
ll& u = x.second;
if (dist[u] < x.first) continue;
for (int i = 0; i < G[u].size(); ++i)
{
Edge& e = G[u][i];
ll& v = e.v;
pair<type,ll> y(dist[u] + e.cost + H[u] - H[v], v);
if (e.cap > 0 && dist[v] > y.first)
{
dist[v] = y.first;
pv[v] = u,pe[v] = i;
q.push(y);
}
}
}
if (dist[t] == INF)
return false;
for (int i = 0; i <= n; ++i)
H[i] += dist[i];
ll f = INF;
for (int v = t; v != s; v = pv[v])
f = std::min(f, G[pv[v]][pe[v]].cap);
flow += f;
cost += f * H[t];
for (int v = t; v != s; v = pv[v])
{
Edge& e = G[pv[v]][pe[v]];
e.cap -= f;
G[v][e.rev].cap += f;
}
return true;
}
ll solve(int s, int t)
{
this->s = s, this->t = t;
flow = cost = 0;
std::fill(H, H + n + 1, 0);
while (dijkstra());
return flow;
}
} mm;
|
BF费用流
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
| struct MCMF
{
struct Edge
{
int from, to, cap, flow, cost;
Edge(int u, int v, int c, int f, int w)
: from(u), to(v), cap(c), flow(f), cost(w) {}
};
int n, m;
vector<Edge> edges;
vector<int> G[maxn];
int inq[maxn];
int d[maxn];
int p[maxn];
int a[maxn];
void init(int n)
{
this->n = n;
for (int i = 0; i <= n; i++)
G[i].clear();
edges.clear();
}
void AddEdge(int from, int to, int cap, int cost)
{
edges.push_back(Edge(from, to, cap, 0, cost));
edges.push_back(Edge(to, from, 0, 0, -cost));
m = edges.size();
G[from].push_back(m - 2);
G[to].push_back(m - 1);
}
bool BellmanFord(int s, int t, int& flow, ll& cost)
{
for (int i = 0; i < n; i++)
d[i] = inf;
memset(inq, 0, sizeof(inq));
d[s] = 0;
inq[s] = 1;
p[s] = 0;
a[s] = inf;
queue<int> q;
q.push(s);
while (!q.empty())
{
int u = q.front();
q.pop();
inq[u] = 0;
for (int i = 0; i < G[u].size(); i++)
{
Edge& e = edges[G[u][i]];
if (e.cap > e.flow && d[e.to] > d[u] + e.cost)
{
d[e.to] = d[u] + e.cost;
p[e.to] = G[u][i];
a[e.to] = min(a[u], e.cap - e.flow);
if (!inq[e.to])
{
q.push(e.to);
inq[e.to] = 1;
}
}
}
}
if (d[t] == inf)
return false;
flow += a[t];
cost += (ll)d[t] * (ll)a[t];
for (int u = t; u != s; u = edges[p[u]].from)
{
edges[p[u]].flow += a[t];
edges[p[u] ^ 1].flow -= a[t];
}
return true;
}
int MincostMaxflow(int s, int t, ll& cost)
{
int flow = 0;
cost = 0;
while(BellmanFord(s, t, flow, cost));
return flow;
}
} mm;
|
对偶图最小割
最大流
太空飞行计划问题(最小割,收益最大问题)
最优收益 = 所有实验的报酬总和 - 该图的最大流
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| int m,n;
scanf("%d%d",&m,&n);
int s=0,t=m+n+1,sum=0;
di.init(t);
for(int i=1;i<=m;i++)
{
int profit,equ;
scanf("%d",&profit);
sum+=profit;
di.AddEdge(s,i,profit);
while(1)
{
char ch;
scanf("%d%c",&equ,&ch);
di.AddEdge(i,m+equ,inf);
if(ch=='\r'||ch=='\n')
break;
}
}
for(int i=1;i<=n;i++)
{
int cost;
scanf("%d",&cost);
di.AddEdge(m+i,t,cost);
}
int ans=di.Maxflow(s,t);
for(int i=1;i<=m;i++)
{
if(di.d[i])
printf("%d ",i);
}
putchar('\n');
for(int i=1;i<=n;i++)
{
if(di.d[m+i])
printf("%d ",i);
}
printf("\n%d\n",sum-ans);
|
建图后跑最大流求出最小割,满流的实验边割掉,满流的设备边也在割集里(但是这是需要购买的),该最小割即为最小亏损。
所以最后一次BFS,所有未被割掉的实验为非饱和弧,可以求出深度。
所以未被割掉的实验(及选择去做的实验)所连接的设备同样可以求出深度。
最小路径覆盖问题(最大流,最小不相交路径覆盖模型,要求路径数最少,路径输出)
二分图定理之一:最小路径覆盖数=顶点数-最大匹配。
覆盖所有的边:每条边下界设为1, 然后求最小流。 覆盖所有的点:建立二分图,对于$u\rightarrow v$的边,看做二分图中的$<u,v>$,然后答案为点数-最大匹配。
不要使用炸点优化!!!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
|
const int maxn = 13005;
const int inf=0x3f3f3f3f;
int nex[maxn];
bool vist[maxn];
int all;
struct Dinic
{
struct Edge
{
int from, to, cap, flow;
Edge(int u, int v, int c, int f):
from(u), to(v), cap(c), flow(f) {}
};
int n, m, s, t;
vector<Edge> edges;
vector<int> G[maxn];
bool vis[maxn];
int d[maxn];
int cur[maxn];
void init(int n)
{
this->n = n;
for (int i = 0; i <= n; i++)
G[i].clear();
edges.clear();
}
inline void AddEdge(int from, int to, int cap)
{
edges.emplace_back(Edge(from, to, cap, 0));
edges.emplace_back(Edge(to, from, 0, 0));
this->m = edges.size();
G[from].push_back(m - 2);
G[to].push_back(m - 1);
}
bool BFS()
{
memset(vis, 0, sizeof(vis));
memset(d, 0, sizeof(d));
queue<int> q;
q.push(s);
d[s] = 0;
vis[s] = 1;
while (!q.empty())
{
int x = q.front();
q.pop();
for (int i = 0; i < G[x].size(); i++)
{
Edge& e = edges[G[x][i]];
if (!vis[e.to] && e.cap > e.flow)
{
vis[e.to] = 1;
d[e.to] = d[x] + 1;
q.push(e.to);
}
}
}
return vis[t];
}
int DFS(int x, int a)
{
if (x == t || a == 0)
return a;
int flow = 0, f;
for (int& i = cur[x]; i < G[x].size(); i++)
{
Edge& e = edges[G[x][i]];
if (d[x] + 1 == d[e.to] && (f = DFS(e.to, min(a, e.cap - e.flow))) > 0)
{
if(x!=s)
{
nex[x]=e.to;
vist[e.to-all]=1;
}
e.flow += f;
edges[G[x][i] ^ 1].flow -= f;
flow += f;
a -= f;
if (a == 0)
break;
}
}
return flow;
}
int Maxflow(int s, int t)
{
this->s = s, this->t = t;
int flow = 0;
while (BFS())
{
memset(cur, 0, sizeof(cur));
flow += DFS(s,inf);
}
return flow;
}
} di;
int main()
{
int n,m;
memset(vist,0,sizeof(vist));
cin>>n>>m;
all=n;
int s=0,t=2*n+1;
di.init(t);
for(int i=1;i<=n;i++)
{
di.AddEdge(s,i,1);
di.AddEdge(n+i,t,1);
}
for(int i=1;i<=m;i++)
{
int u,v;
cin>>u>>v;
di.AddEdge(u,n+v,1);
}
int ans=di.Maxflow(s,t);
for(int i=1;i<=n;i++)
{
if(!vist[i])
{
int now=i;
cout<<now<<' ';
while(nex[now]&&nex[now]!=t)
{
cout<<nex[now]-n<<' ';
now=nex[now]-n;
}
cout<<endl;
}
}
cout<<n-ans<<endl;
return 0;
}
|
P2774 方格取数问题(最大流,最小割)
m*n 个方格棋盘中,每个方格中有一个正整数。从方格中取数,使任意 2 个数所在方格没有公共边,且取出的数的总和最大。
思路:黑白染色,按奇偶性建立二分图,奇连s,偶连t。枚举每个奇数性质的方格,连接相邻的偶数性质的方格。跑dinic求出最小割,总值减去最小割即为答案。
带权最大独立集=所有点的点权-最小割。因为是最小割的剩余图,所以剩下的点之间不会有联系,即为符合要求的答案。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| int main()
{
int m,n;
scanf("%d%d",&m,&n);
int s=0,t=m*n+1,sum=0;
di.init(t+1);
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
int val,no;
scanf("%d",&val);
sum+=val;
no=n*(i-1)+j;
if((i+j)%2){
di.AddEdge(s,no,val);
}
else{
di.AddEdge(no,t,val);
}
}
}
int nx[4]={0,-1,0,1};
int ny[4]={-1,0,1,0};
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
{
int no=n*(i-1)+j;
if((i+j)%2){
for(int k=0;k<4;k++)
{
int x=i+nx[k],y=j+ny[k];
if(x<=0||x>m||y<=0||y>n)
continue;
int no2=n*(x-1)+y;
di.AddEdge(no,no2,inf);
}
}
}
printf("%d\n",sum-di.Maxflow(s,t));
return 0;
}
|
费用流
P4012 深海机器人问题(物品在网格上)
物品在网格的边上,每条网格的边有权值,交叉点作为节点,在图上添加点和点之间的边,设容量为1,花费为-cost。
注意设置容量inf,费用为0的经过边,跑最小费用最大流,答案取负。
P3356 火星探险问题(物品在交叉点上)
物品在节点上,而且有障碍。
思路:拆点,若不为障碍,拆点间添加容量为inf,价值为0的边;若该点有所需物品,两点间额外添加一条容量为1价值为-val的边;
跑最小费用最大流即可,使用DFS输出路径。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| for(int i=1;i<=n;i++)
{
flag=0;
mm.dfs(1,1,1,i);
}
void MCMF::dfs(int x,int y,int u,int no)
{
int kx,ky,dir;
int res=p*q+u;
if(flag)
return;
for(int i=0;i<G[res].size();i++)
{
if(flag)
return;
if(edges[G[res][i]].flow>0&&(edges[G[res][i]].to==u+1||edges[G[res][i]].to==u+p))
{
edges[G[res][i]].flow--;
if(edges[G[res][i]].to==u+1)
dir=1;
else
dir=0;
printf("%d %d\n",no,dir);
if(dir==1)
dfs(x,y+1,u+1,no);
else
dfs(x+1,y,u+p,no);
if(edges[G[res][i]].to==p*q)
flag=1;
}
}
}
|
问题:给出DAG每条边的容量和扩容费用,1.求出1到n的最大流。2.求出1到n的最大流增加K所需的最小扩容费用。
先跑一个零费用最大流。利用残余网络进行费用流扩容,将原来的0费用网络添加新的费用边,并进行限流,cost即为扩容费用。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| int n,m,k;
cin>>n>>m>>k;
mm.init(n+10);
for(int i=1;i<=m;i++){
cin>>e[i].u>>e[i].v>>e[i].c>>e[i].w;
mm.AddEdge(e[i].u,e[i].v,e[i].c,0);
}
ll cost;
cout<<mm.MincostMaxflow(1,n,cost)<<' ';
for(int i=1;i<=m;i++)
mm.AddEdge(e[i].u,e[i].v,inf,e[i].w);
int s=0;
mm.AddEdge(s,1,k,0);
mm.MincostMaxflow(s,n,cost);
cout<<cost<<endl;
|


.png)