数据结构代码模板

发表于 更新于 分类于 阅读次数：

这里记录了数据结构方面平时个人常用的代码模板。

数据结构

单调数据结构

  • 数组某一个值作为区间极值的区间长度：单调栈处理L、R数组CF547B.
  • 求$k$长限制下最大子段和：单调队列维护递增前缀和，P1714.
  • 对数字保持相对顺序去重并使字典序最大：，Maximize the Remaining String.

单调栈求每一元素作为区间极值的端点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
int a[maxn],ans[maxn],stk[maxn],top=0,l[maxn],r[maxn];
signed main(signed argc, char const *argv[])
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>a[i],r[i]=n;
    for(int i=1;i<=n;i++)
    {
        while(top&&a[stk[top]]>=a[i])
        {
            r[stk[top]]=i-1;//确定栈顶的右端点
            top--;
        }
        l[i]=stk[top]+1;//栈顶元素小于a[i],[stk[top]+1,
        stk[++top]=i;
    }
    for(int i=1;i<=n;i++)
    {
        int len=r[i]-l[i]+1;
        ans[len]=max(ans[len],a[i]);
    }
    for(int i=n-1;i>=1;i--)
        ans[i]=max(ans[i],ans[i+1]);
    for(int i=1;i<=n;i++)
        cout<<ans[i]<<' ';
    return 0;
}
/*
 *n个小熊站成一排,每个都有一个高度ai。
 *对于一个区间[L,R],定义该区间的strength值为:该区间的最小值。
 *对于相同长度的区间strength值中的最大值为多少
 *从len=1开始输出。肯定是单调递减的
 *求所有k长区间最大最小值
 *应该是维护最小值,弹出时根据长度更新答案
 *维护一个单调递增的栈
*/

对数字保持相对顺序去重并使字典序最大

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
char s[maxn],stk[maxn];
int top;
signed main(signed argc, char const *argv[])
{
    int t,n;
    cin>>t;
    while(t--)
    {
        cin>>s+1;
        top=0;
        int n=strlen(s+1);
        map<char,int>last;
        for(int i=1;i<=n;i++)
            last[s[i]]=i;
        map<char,bool> vis;
        for(int i=1;i<=n;i++)
        {
            if(vis[s[i]])
                continue;
            while(stk[top]<s[i]&&i<last[stk[top]])//不是最后一个
                vis[stk[top--]]=0;
            stk[++top]=s[i];
            vis[s[i]]=1;
        }
        stk[top+1]='\0';
        cout<<stk+1<<endl;
    }
    return 0;
}
/*
 *原题:https://blog.nowcoder.net/n/2b1c2c0ffc9045719f8dfdf4a4aeabfb?f=comment
*/

树状数组

一种天才的数据结构，利用了二进制下标来控制区间范围，构造了一种类似二叉树的数据结构，使得空间复杂度仍为$O(n)$的情况下，对于区间前缀和的查询时间复杂度达到了$O(logn)$。

img

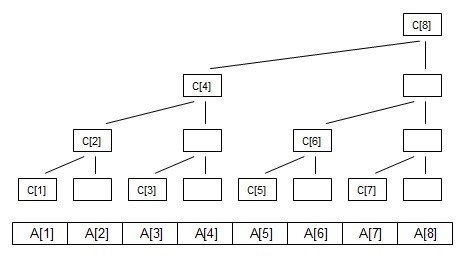
在树状数组中，每一个下标为$x$的节点，都保存着在$[x-2^k+1,x]$的区间和，$k$为$x$二进制末尾$0$的个数。

可进行区间修改区间查询的bit模板

和单点修改并查询前缀和的实现思路略有不同。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
struct BinaryIndexedsTree
{
    int n;
    ll c[maxn],sum[maxn];//c维护差分数组,sum维护i*c[i]的前缀和
    inline int lowbit(int x)
    {
        return x & (-x);
    }
    void build(int *a,int n)//a是原数组,n是元素个数
    {
        this->n=n;
        memset(c,0,sizeof(c));
        memset(sum,0,sizeof(sum));
        for(int i=1;i<=n;i++)
            add(i,a[i]-a[i-1]);//构建差分c数组
    }
    void add(int k,ll val)//修改:a[k]加上val,直接在c数组上操作
    {//请使用区间更新,不要使用这个函数
        for(int i=k;i<=n;i+=lowbit(i))//从叶子一直更新到根节点
            c[i]+=val,sum[i]+=val*(k-1);//每个节点都加上val
    }
    void radd(int l,int r,ll val)//区间更新
    {
        add(l,val);//把l之后所有的点都更新一遍
        add(r+1,-val);//因为r之后的点是不用更新的,但是多更新了,所以要每个点都-val；
    }
    ll query(int k)//查询:c[i]前缀和的前缀和,即a[i]的前缀和
    {//节点i的长度为lowbit(i)
        ll ret=0;
        for(int i=k;i;i-=lowbit(i))
            ret+=k*c[i]-sum[i];
        return ret;
    }
} bit;

二维树状数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
struct BinaryIndexedsTree2D
{
    #define lowbit(x) ((x) & -(x))
    int n,m;//行与列
    ll t1[maxn][maxn], t2[maxn][maxn], t3[maxn][maxn], t4[maxn][maxn];
    void add(ll x, ll y, ll z)
    {
        for(int i=x;i<=n;i+=lowbit(i))
            for(int j=y;j<=m;j+=lowbit(j))
            {
                t1[i][j]+=z;
                t2[i][j]+=z*x;
                t3[i][j]+=z*y;
                t4[i][j]+=z*x*y;
            }
    }
    void radd(ll xa,ll ya,ll xb,ll yb,ll z)
    {//(xa,ya)到(xb,yb)的矩形全部增加z
        add(xa,ya,z);
        add(xa,yb+1,-z);
        add(xb+1,ya,-z);
        add(xb+1,yb+1,z);
    }
    void build(int n,int m,ll a[][maxn])
    {//用给定的数组a初始化
        memset(t1,0,sizeof(t1));
        memset(t2,0,sizeof(t2));
        memset(t3,0,sizeof(t3));
        memset(t4,0,sizeof(t4));
        this->n=n,this->m=m;
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
                radd(i,j,i,j,a[i][j]);
    }
    void build(int n,int m)
    {//初始全为0
        memset(t1,0,sizeof(t1));
        memset(t2,0,sizeof(t2));
        memset(t3,0,sizeof(t3));
        memset(t4,0,sizeof(t4));
        this->n=n,this->m=m;
    }
    ll ask(ll x,ll y)
    {
        ll res = 0;
        for(int i=x;i;i-=lowbit(i))
            for(int j=y;j;j-=lowbit(j))
                res += (x + 1) * (y + 1) * t1[i][j]
                    - (y + 1) * t2[i][j]
                    - (x + 1) * t3[i][j]
                    + t4[i][j];
        return res;
    }
    ll query(ll xa, ll ya, ll xb, ll yb)
    {//查询(xa,ya)到(xb,yb)的矩形权值之和
        return ask(xb,yb)-ask(xb,ya-1)-ask(xa-1,yb)+ask(xa-1,ya-1);
    }
} b2d;

三维树状数组求前缀最大值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
struct BinaryIndexTree
{
    using type = int;
    type c[maxn];
    int n, m, h;
    void init(int n, int m, int h)
    {
        memset(c, -0x3f, sizeof(c));
        this->n = n;
        this->m = m;
        this->h = h;
    }
#define lowbit(x) ((x) & (-x))
    int id(int x, int y, int z){return x*m*h + y*h + z;}
    void update(int x, int y, int z, type val)
    {
        for(int i = x; i <= n; i += lowbit(i))
            for(int j = y; j <= m; j += lowbit(j))
                for(int k = z; k <= h; k += lowbit(k))
                    c[id(i, j, k)] = max(c[id(i, j, k)], val);
    }
    type query(int x, int y, int z)
    {
        type ans = -inf;
        for(int i = x ; i; i -= lowbit(i))
            for(int j = y; j; j -= lowbit(j))
                for(int k = z; k; k -= lowbit(k))
                    ans = max(ans, c[id(i, j, k)]);
        return ans;        
    }
} bit[8];

树状数组实现平衡树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
struct BITth
{
    int n,m,c[maxn+1],a[maxn+1];
    void init(int s){
        m=(int)(log(n=s)/log(2));
        memset(c,0,sizeof(c)); memset(a,0,sizeof(a));
    }
    void change(int p, int k) {for(;p<=n;p+=p&-p) c[p]+=k;}
    int sum(int p) {int s=0; for(;p;p-=p&-p) s+=c[p]; return s;}//维护前缀数量和
    void ins(int x) {a[x]++; change(x,1);};//插入一个x
    void del(int x) {if (a[x]--) change(x,-1); else a[x]=0;}//删除一个x
    bool find(int x) {return a[x];}//查找x是否存在
    int rank(int x) {return sum(x-1)+1;}//x的排名,从0开始
    int select(int k){//第k小,k从0开始
        int p=0,s=0;
        if(sum(n)<k) return -1;//不存在
        for(int i=(1<<m);i;i>>=1)
            if (p+i<=n&&s+c[p+i]<=k) {p+=i; s+=c[p];}
        return p+1;
    }
    int select_b(int k){//二分查第k大
        int l=1,r=n,mid;
        if(sum(n)<k) return -1;
        for(mid=l+r>>1;l<r;mid=l+r>>1)
            if(sum(mid)<k)
                l=mid+1; else r=mid;
        return l;
    }
    int pred(int x) {return select(sum(x-1));}//x的上一个元素
    int succ(int x) {return select(sum(x)+1);}//x的下一个元素
} bit1;

01字典树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
class Trie01
{
public:
    static const int maxm=2,start=30;//字符范围
    int trie[maxn][maxm],path[maxn][maxm],isw[maxn],siz;//节点数siz
    int lazy[36];
    void init()
    {
        siz=1;
        memset(lazy,0,sizeof(lazy));
        memset(path,0,sizeof(path));
        memset(trie[0],0,sizeof(trie[0]));
        memset(isw,0,sizeof(isw));
    }
    void insert(const int &key)
    {//插入一个key
        int rt=0;
        for(int i=start;i>=0;i--)
        {
            int id=(key>>i)&1;
            if(!trie[rt][id])
            {
                memset(trie[siz],0,sizeof(trie[siz]));
                trie[rt][id]=siz++;//添加新节点
            }
            path[rt][id]++;//子节点多少个
            rt = trie[rt][id];//向下
        }
        isw[rt]++;
    }
    int qmin(const int &key)
    {//查询异或最小值(考虑xor操作)
        int rt=0,ret=0;
        for(int i=start;i>=0;i--)
        {
            int id=(key>>i)&1,nex=0;//最好是相同的,异或为0,答案更小
            id^=lazy[i];//看这一位有没有被反转
            if(path[rt][id]==0)//这种情况莫得了
                id^=1,nex=1;//id换较差的那种//该位的贡献1
            ret=(ret<<1)+nex;
//            path[rt][id]--;//该边数量减1
            rt=trie[rt][id];//向下
        }
        return ret^key;
    }
    void Xor(const int &key)
    {//所有值全部异或key
        for(int i=start;i>=0;i--)
        {//如果该边被对调,标记在其父结点上
            int id=(key>>i)&1;
            lazy[i]^=id;//1反转,该深度所有点都被标记
        }
    }
    int mex()
    {//查询不在键值集合内的最小值
        int rt=0,ret=0;//
        for(int i=start;i>=0;i--)
        {//0边子树非满走0边
            int id=lazy[i],nex=0;//是否被对调,id那边是现在的0
            if(path[rt][id]>=(1<<i))//最优的那边满了,叶子点数=2^i
                id^=1,nex=1;//走id的另一边//该位的贡献为1
            ret=(ret<<1)+nex;
            if(!trie[rt][id])//这边的子树还没有点,都可以取最小的
            {
                ret<<=i;
                break;
            }
            rt=trie[rt][id];
        }
        return ret;
    }
} tt;
signed main(signed argc, char const *argv[])
{
    int n,m,key;
    cin>>n>>m;
    vector<int> f(n);
    for(auto &i:f)
        cin>>i;
    sort(f.begin(),f.end());
    f.erase(unique(f.begin(),f.end()),f.end());
    tt.init();
    for(auto &i:f)
        tt.insert(i);
    while(m--)
    {
        cin>>key;
        tt.Xor(key);
        cout<<tt.mex()<<endl;
    }
    return 0;
}
/*
 * 2021-05-02-10.49.26
 * 整体异或代表01字典树左右子树对调,自底向上
 * 如果异或key值该位为1,对该深度打一个标记
 * 否则如果递归反转的话,复杂度指数级的
 * 为查询mex,似乎要在字典树中递归计数,看节点是不是满的
*/

普通线段树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
struct SegTreeForMax
{//用来进行区间推平,以及区间最值
    using type = int;
    struct SegTreeNode
    {
        type val,lazy;//延迟标记:储存节点的修改情况
        SegTreeNode(){
            val=lazy=0;
        }
    } Tree[maxn<<2];//完全二叉树(有没用到的节点),一倍可能炸
    type MIN=-1;
    int L=1,R=maxn-1,root=1;
    inline void pushup(int rt)
    {
        Tree[rt].val=max(Tree[rt<<1].val,Tree[rt<<1|1].val);
    }
    inline void pushdown(int rt,int l,int r)
    {
        if(Tree[rt].lazy!=MIN)
        {
            Tree[rt<<1].lazy=Tree[rt<<1|1].lazy=Tree[rt].lazy;
            Tree[rt<<1].val=Tree[rt<<1|1].val=Tree[rt].lazy;
            Tree[rt].lazy=MIN;
        }
    }
    void build(int rt,int l,int r)
    {
        Tree[rt].lazy=Tree[rt].val=0;
        if(l==r)
        {
            return;
        }
        int mid=(l+r)>>1;
        build(rt<<1,l,mid);
        build(rt<<1|1,mid+1,r);
        pushup(rt);
    }
    void init(int n)
    {
        this->L=1;
        this->R=n;
        this->root=1;
        build(1,1,n);
    }
    void modify(int l,int r,type val,int rt,int nl,int nr)
    {//目标更新区间[l,r]
        if(l>nr||r<nl)
            return;
        if(l<=nl&&nr<=r)
        {
            Tree[rt].val=val;
            Tree[rt].lazy=val;
            return;
        }
        pushdown(rt,nl,nr);
        int mid=(nl+nr)>>1;
        modify(l,r,val,rt<<1,nl,mid);
        modify(l,r,val,rt<<1|1,mid+1,nr);
        pushup(rt);
    }
    type query(int l,int r,int rt,int nl,int nr)
    {
        if(l>nr||r<nl)
            return MIN;
        if(l<=nl&&nr<=r)
            return Tree[rt].val;
        pushdown(rt,nl,nr);
        int mid=(nl+nr)>>1;
        return max(query(l,r,rt<<1,nl,mid),query(l,r,rt<<1|1,mid+1,nr));
    }
} stm;

动态开点线段树

该模板的区间推平操作有问题，请尽量避免使用assign。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
struct SegTree
{
    /*
     * 动态开点线段树,可区间修改区间查询,能够处理零或负数位置
     * 不需要build,用在没有提供初始数据的场合/强制在线无法离散化建树
     * 默认初始值为0,有初始值可以单点修改
    */
    using type = int;
    struct node
    {//
        int ls,rs;
        type val,mark,MAX;
        node(){}
        node(int l,int r,type v):
            ls(l),rs(r),val(v),MAX(v){mark=0;}
    } tree[maxn<<2];
    #define ls(x) tree[x].ls
    #define rs(x) tree[x].rs
    int cnt=1;
    const type NA = 0;
    static const int L=1,R=2e6+10;
    type pushup(type a,type b)
    {//修改之后的递归向上更新
        return a+b;
    }
    void update(int x,type d,int len)
    {//区间更新
        tree[x].val += d*len;
        tree[x].MAX += d;
        tree[x].mark += d;
    }
    void pushdown(int x,int len)
    {
        if(!ls(x))//左儿子不存在,创建新节点
            ls(x)=++cnt;
        if(!rs(x))//右儿子不存在
            rs(x)=++cnt;
        if(tree[x].mark!=NA)
        {
            update(ls(x),tree[x].mark,len/2);
            update(rs(x),tree[x].mark,len-len/2);
            tree[x].mark=NA;
        }
    }
    void assign(int l,int r,type val,int x=1,int cl=L,int cr=R)
    {//区间[l,r]推平,整体赋值为val,不规范,不要使用
        if(cl>=l&&cr<=r)
        {
            tree[x].val=(cr-cl+1)*val;
            tree[x].mark=val;
            tree[x].MAX=val;
            return;
        }
        pushdown(x,cr-cl+1);
        int mid=(cl+cr-1)/2;
        if(mid>=l)
            assign(l,r,val,ls(x),cl,mid);
        if(mid<r)
            assign(l,r,val,rs(x),mid+1,cr);
        tree[x].val=pushup(tree[ls(x)].val,tree[rs(x)].val);//pushup操作
        tree[x].MAX=max(tree[ls(x)].MAX,tree[rs(x)].MAX);
    }
    void modify(int l,int r,type d,int x=1,int cl=L,int cr=R)
    {//目标区间[l,r],整体增加d,当前节点x,当前区间[cl,cr]
        if(cl>=l&&cr<=r)
            return update(x,d,cr-cl+1);//注意这个return
        pushdown(x,cr-cl+1);
        int mid=(cl+cr-1)/2;
        if(mid>=l)
            modify(l,r,d,ls(x),cl,mid);
        if(mid<r)
            modify(l,r,d,rs(x),mid+1,cr);
        tree[x].val=pushup(tree[ls(x)].val,tree[rs(x)].val);//pushup操作
        tree[x].MAX=max(tree[ls(x)].MAX,tree[rs(x)].MAX);
    }
    type querysum(int l,int r,int x=1,int cl=L,int cr=R)
    {//查询[l,r]区间权值和,当前节点x,当前区间[cl,cr]
        if(cl>=l&&cr<=r)//询问区间被当前区间包含
            return tree[x].val;
        pushdown(x,cr-cl+1);
        int mid=(cl+cr-1)/2;
        if(mid>=r)//在[cl,cr]的左半区间询问
            return querysum(l,r,ls(x),cl,mid);
        else if(mid<l)//在右半
            return querysum(l,r,rs(x),mid+1,cr);
        tree[x].MAX=max(tree[ls(x)].MAX,tree[rs(x)].MAX);
        return pushup(querysum(l,r,ls(x),cl,mid),querysum(l,r,rs(x),mid+1,cr));
    }
    type querymax(int l,int r,int x=1,int cl=L,int cr=R)
    {//查询区间[l,r]最大值
        if(cl>=l&&cr<=r)//[cl,cr]在询问区间内
            return tree[x].MAX;
        pushdown(x,cr-cl+1);
        int mid=(cl+cr-1)/2;
        if(mid>=r)
            return querymax(l,r,ls(x),cl,mid);
        else if(mid<l)//在右半
            return querymax(l,r,rs(x),mid+1,cr);
        tree[x].val=pushup(tree[ls(x)].val,tree[rs(x)].val);
        return max(querymax(l,r,ls(x),cl,mid),querymax(l,r,rs(x),mid+1,cr));
    }
    type ask4firstgreat(int l,int r,type val,int x=1,int cl=L,int cr=R)
    {//在区间[l,r]查询第一个>val的值的下标,当前区间[cl,cr]
        if(cl>cr)//越界
            return -1;
        if(cl==cr)//叶子
            return (tree[x].MAX>val?cl:-1);
        if(l<=cl&&cr<=r&&tree[x].MAX<=val)//该区间最值<=val,不存在
            return -1;
        pushdown(x,cr-cl+1);
        int mid=(cl+cr-1)/2,p=-1;
        if(l<=mid)//[cl,mid]与[l,r]有交集
            p=ask4firstgreat(l,r,val,ls(x),cl,mid);
        if(p==-1&&mid+1<=r)//左子树未找到,且[mid+1,cr]
            p=ask4firstgreat(l,r,val,rs(x),mid+1,cr);
        tree[x].val=pushup(tree[ls(x)].val,tree[rs(x)].val);//pushup操作
        tree[x].MAX=max(tree[ls(x)].MAX,tree[rs(x)].MAX);
        return p;
    }
    type ask4lastgreat(int l,int r,type val,int x=1,int cl=L,int cr=R)
    {//在区间[l,r]查询最后一个>val的值的下标,当前区间[cl,cr]
        if(cl>cr)
            return -1;
        if(cl==cr)
            return (tree[x].MAX>val?cl:-1);
        if(l<=cl&&cr<=r&&tree[x].MAX<=val)//该区间最值<=val,不存在
            return -1;
        pushdown(x,cr-cl+1);
        int mid=(cl+cr-1)/2,p=-1;
        if(mid+1<=r)
            p=ask4lastgreat(l,r,val,rs(x),mid+1,cr);
        if(p==-1&&l<=mid)
            p=ask4lastgreat(l,r,val,ls(x),cl,mid);
        tree[x].val=pushup(tree[ls(x)].val,tree[rs(x)].val);//pushup操作
        tree[x].MAX=max(tree[ls(x)].MAX,tree[rs(x)].MAX);
        return p;
    }
    #undef ls
    #undef rs
} T;

可持久化权值线段树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+5;
int a[maxn];
vector<int> v;
inline int getid(int x)
{
    return lower_bound(v.begin(),v.end(),x)-v.begin()+1;
}
struct node
{//左右子树节点编号,区间上数量为sum
    int l,r,sum;
} hjt[maxn<<5];
int cnt,root[maxn];//内存值计数器,root[i]为根节点编号(在之前基础上插入a[i]的树)
void Insert(int l,int r,int pre,int &now,int p)//p为新加入权值(也为位置)
{//对离散化后范围[l,r]建树,pre:上一个版本的编号,now:当前版本的编号
    //找到新加入权值对应节点,更新该节点信息
    hjt[++cnt]=hjt[pre];//动态开点:上一个版本对应位置节点复制一份,新树中添加lgn个节点
    now=cnt;//当前节点编号等于新分配
    hjt[now].sum++;//插入,数量++,维护离散化后值域[l,r]上的个数
    if(l==r)
        return;
    int mid=(l+r)>>1;
    if(p<=mid)//插入到左子树
        Insert(l,mid,hjt[pre].l,hjt[now].l,p);
    else//插入到右子树上
        Insert(mid+1,r,hjt[pre].r,hjt[now].r,p);
}
int query(int l,int r,int L,int R,int k)
{//[l,r]:离散化后查询范围,L/R:树的版本编号
    if(l==r)//叶子节点
        return l;
    int mid=(l+r)>>1;
    /*
     前缀和思想,求出[1,r]的数量
     用r版本减去l-1版本的同一区间信息,得到指定查询区域[l,r]的线段树
     */
    //新减出来的差值树上,左子树数值
    int tmp=hjt[hjt[R].l].sum-hjt[hjt[L].l].sum;//
    if(k<=tmp)//第k大在左子树上
        query(l,mid,hjt[L].l,hjt[R].l,k);
    else
        query(mid+1,r,hjt[L].r,hjt[R].r,k-tmp);
}
int main()//区间第k大
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        v.push_back(a[i]);
    }
    sort(v.begin(),v.end());
    v.erase(unique(v.begin(),v.end()),v.end());//对v去重
    for(int i=1;i<=n;i++)//维护离散化后的值域上个数
    {//思想:保存插入时的历史版本,对每个前缀建树(n棵)
        Insert(1,v.size(),root[i-1],root[i],getid(a[i]));
    }//第i棵存储前i个值出现次数
    while(m--)
    {
        int l,r,k;
        cin>>l>>r>>k;//[l,r]不是数值范围,是数列上给定区间,即a[l:r]上第k大
        cout<<v[query(1,n,root[l-1],root[r],k)-1]<<endl;
    }
    return 0;
}

替罪羊树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
const int maxn=1E5+5;
const double alpha=0.75;
struct node
{
    int l,r,val;
    int siz,fact;
    bool exist;
} tzy[maxn];
int cnt,root;
void newnode(int &now,int val)//新建节点
{
    now=++cnt;
    tzy[now].val=val;
    tzy[now].siz=tzy[now].fact=1;
    tzy[now].exist=1;
}
bool imbalence(int now)
{
    if(max(tzy[tzy[now].l].siz,tzy[tzy[now].r].siz)>tzy[now].siz*alpha)
        return 1;//最大子树大小大于now*平衡因子
    if(tzy[now].siz-tzy[now].fact>tzy[now].siz*0.3)
        return 1;//已删除节点超过30%
    return 0;
}
vector<int> v;//储存重构树中未删除节点中序遍历编号(有序)
void ldr(int now)//中序遍历
{
    if(!now)
        return;
    ldr(tzy[now].l);
    if(tzy[now].exist)//舍弃所有删除点
        v.push_back(now);
    ldr(tzy[now].r);
}
void lift(int l,int r,int &now)
{
    if(l==r)//叶子节点
    {
        now=v[l];
        tzy[now].l=tzy[now].r=0;//子节点不存在
        tzy[now].siz=tzy[now].fact=1;
        return;
    }
    int mid=(l+r)>>1;
    while(mid&&l<mid&&tzy[v[mid]].val==tzy[v[mid-1]].val)
        mid--;//将相同元素都放在右子树
    now=v[mid];//修改父节点连接的左右子树
    if(l<mid)
        lift(l,mid-1,tzy[now].l);//这里面传递左右引用下去,会自动修改节点间的父子关系
    else
        tzy[now].l=0;
    lift(mid+1,r,tzy[now].r);//因为向下取整,右子树一定存在
    tzy[now].siz=tzy[tzy[now].l].siz+tzy[tzy[now].r].siz+1;
    tzy[now].fact=tzy[tzy[now].l].fact+tzy[tzy[now].r].fact+1;
}
void rebuild(int &now)//暴力重构
{
    v.clear();
    ldr(now);//中序遍历
    if(v.empty())
    {
        now=0;
        return;
    }
    lift(0,v.size()-1,now);//从中间拎起来
}
void update(int now,int ed)//头递归自底向上更新siz信息
{
    if(!now)
        return;
    if(tzy[ed].val<tzy[now].val)
        update(tzy[now].l,ed);
    else
        update(tzy[now].r,ed);
    tzy[now].siz=tzy[tzy[now].l].siz+tzy[tzy[now].r].siz+1;
}
void check(int &now,int ed)//从根节点一直检查到ed
{
    if(now==ed)
        return;
    if(imbalence(now))//不平衡
    {
        rebuild(now);//暴力重构
        update(root,now);//向上更新siz信息
        return;
    }
    if(tzy[ed].val<tzy[now].val)
        check(tzy[now].l,ed);//检查受更新影响的子树是否需要重构
    else
        check(tzy[now].r,ed);
}
void ins(int &now,int val)//插入,传递引用
{
    if(!now)//到了叶子节点下面
    {
        newnode(now,val);//这里修改了now的值,相当于父节点的"指针"指向这里
        check(root,now);//检查是否需要重构
        return;
    }
    tzy[now].siz++;
    tzy[now].fact++;
    if(val<tzy[now].val)//比当前值小
        ins(tzy[now].l,val);//向当前节点左子树插入
    else
        ins(tzy[now].r,val);//否则插到右子树
}
void del(int now,int val)//删除
{
    if(tzy[now].exist&&tzy[now].val==val)//找到
    {
        tzy[now].exist=0;
        tzy[now].fact--;//实际大小-1
        check(root,now);//从根节点开始检查是否失衡
        return;
    }
    tzy[now].fact--;//所有祖先节点实际大小--
    if(val<tzy[now].val)//向下找
        del(tzy[now].l,val);
    else
        del(tzy[now].r,val);
}
int getrank(int val)//查询val的排名
{
    int now=root,rak=1;
    while(now)//
    {
        if(val<=tzy[now].val)//val比当前结点权值小
        {
            now=tzy[now].l;//到左子树上查询
        }
        else{//rak+=左子树大小+当前节点是否存在
            rak+=tzy[now].exist+tzy[tzy[now].l].fact;
            now=tzy[now].r;//到右子树查询
        }
    }
    return rak;
}
int getnum(int rak)//查询排名的值
{
    int now=root;
    while(now)
    {
        if(tzy[now].exist&&tzy[tzy[now].l].fact+tzy[now].exist==rak)
            break;//左子树实际大小+当前节点存在==rak,则当前节点即为目标
        else if(tzy[tzy[now].l].fact>=rak)
            now=tzy[now].l;//一定在当前节点左子树,到左子树上查询
        else{//减掉当前个数,到右子树上找
            rak-=tzy[tzy[now].l].fact+tzy[now].exist;
            now=tzy[now].r;
        }
    }
    return tzy[now].val;
}
int main()
{
    int n,ope,x;
    cin>>n;
    while(n--)
    {
        cin>>ope>>x;
        switch(ope)
        {
        case 1:
            ins(root,x);
            break;
        case 2:
            del(root,x);
            break;
        case 3://查询数x的排名
            cout<<getrank(x)<<'\n';
            break;
        case 4://查询排名x的数
            cout<<getnum(x)<<'\n';
            break;
        case 5://给出数,查询前驱
            cout<<getnum(getrank(x)-1)<<'\n';
            break;
        case 6://给一个数,查后继(不一定在树上)
            cout<<getnum(getrank(x+1))<<'\n';
            break;//
        }
    }
    return 0;
}

AVL树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
struct Node
{
    int l,r,val;//左右儿子编号,该点权值
    int height,siz;//高度,树大小
} avl[maxn];
int cnt=0,root=0;//注意初始化
inline void newnode(int &now,int val)
{//新建节点
    avl[now=++cnt].val=val;
    avl[cnt].siz=avl[cnt].height=1;
}
inline void update(int now)
{//更新节点大小和高度
    avl[now].siz=avl[avl[now].l].siz+avl[avl[now].r].siz+1;
    avl[now].height=max(avl[avl[now].l].height,avl[avl[now].r].height)+1;
}
inline int bf(int now)
{//获取平衡因子bf
    return avl[avl[now].l].height-avl[avl[now].r].height;
}
inline void lrotate(int &now)
{//now节点左旋,因为右子树过高
    int r=avl[now].r;//记录右儿子
    avl[now].r=avl[r].l;//右儿子左子树接到now右儿子上
    avl[r].l=now;//now作为r的左子树
    now=r;
    update(avl[now].l),update(now);
}
inline void rrotate(int &now)
{//now右旋
    int l = avl[now].l;
    avl[now].l = avl[l].r;
    avl[l].r = now;
    now = l;
    update(avl[now].r),update(now);
}
inline void check(int &now)
{//检查now是否需要旋转,并更新
    int nowf=bf(now);
    if(nowf>1)
    {//左子树过高
        int lf=bf(avl[now].l);
        if(lf>0)//now左儿子的左子树过高,LL
            rrotate(now);//右旋now节点
        else//now左儿子右子树过高,LR
            lrotate(avl[now].l),rrotate(now);
    }//左旋左儿子,再右旋now
    else if(nowf<-1)
    {//右子树过高
        int rf=bf(avl[now].r);
        if(rf<0)//RR
            lrotate(now);
        else//RL
            rrotate(avl[now].r),lrotate(now);
    }
    else if(now)//平衡且非空
        update(now);
}
void ins(int &now,int val)
{
    if(!now)//不存在则新建
        newnode(now,val);
    else if(val<avl[now].val)
        ins(avl[now].l,val);
    else
        ins(avl[now].r,val);
    check(now);
}
int find(int &now,int fa)
{//找到以id为根的子树上最小的那个点(没有左儿子),并返回编号
    int ret;
    if(!avl[now].l)//没有左儿子了,说明已找到
    {
        ret=now;//相当于这个叶子节点暂时删掉了
        avl[fa].l=avl[now].r;//右子树替换该点,接到父节点左儿子上
    }
    else{
        ret=find(avl[now].l,now);//左子树上继续找
        check(now);//回溯调整
    }
    return ret;//返回找到的节点编号
}
void del(int &now,int val)
{
    if(val==avl[now].val)//要删除的结点
    {
        int l=avl[now].l,r=avl[now].r;
        if(!l||!r)//叶子节点或者只有一个儿子
            now=l+r;//直接将编号改为子节点
        else
        {//在右子树上找后继
            now=find(r,r);//后继替换删除节点位置,连接左右儿子
            if(now!=r)//后继不是删除节点的右儿子,否则本来是连接好的不必更改
                avl[now].r=r;//now右儿子改成删除节点右儿子
            avl[now].l=l;//now左儿子改成删除节点左儿子
        }
    }
    else if(val<avl[now].val)
        del(avl[now].l,val);//左子树上找
    else
        del(avl[now].r,val);//右子树上找
    check(now);//递归回溯检查
}
int getrnk(int val)
{//传入值查询排名
    int now=root,ans=1;
    while(now)//没到达叶子节点
    {
        if(val<=avl[now].val)
            now=avl[now].l;//在now左子树上找
        else{//在右子树上找
            ans+=avl[avl[now].l].siz+1;//左子树与now节点都比val小
            now=avl[now].r;
        }
    }
    return ans;
}
int getval(int rnk)
{
    int now=root;
    while(now)
    {//每轮在now子树上找第rnk大
        if(avl[avl[now].l].siz+1==rnk)
            break;//找到了,now就是
        else if(avl[avl[now].l].siz>=rnk)
            now=avl[now].l;//rnk在左子树上
        else{//减去左子树和now节点,并在右子树上找
            rnk-=avl[avl[now].l].siz+1;
            now=avl[now].r;
        }
    }
    return avl[now].val;
}
signed main()
{
    int n,op,x;
    cin>>n;
    while(n--)
    {
        cin>>op>>x;
        switch(op)
        {
        case 1:
            ins(root,x);
            break;
        case 2:
            del(root,x);
            break;
        case 3://给值查排名
            cout<<getrnk(x)<<endl;
            break;
        case 4://给排名查值
            cout<<getval(x)<<endl;
            break;
        case 5://前驱
            cout<<getval(getrnk(x)-1)<<endl;
            break;
        case 6://后继
            cout<<getval(getrnk(x+1))<<endl;
            break;//可能有多个x,所以要+1
        }
    }
    return 0;
}

Splay

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
const int maxn=2e5+10,inf=0x3f3f3f3f,mod=1000000007;
struct Node
{
    int l,r;//左右儿子编号
    int val,siz;//节点权值,子树大小
    int cnt;//当前节点重复次数,默认为1
} spl[maxn];
int nodecnt,root;//内存池计数器与根结点编号
inline void newnode(int &now,int &val)
{
    spl[now=++nodecnt].val=val;
    spl[now].siz=spl[now].cnt=1;
}
inline void update(int now)
{//更新节点子树大小
    spl[now].siz=spl[spl[now].l].siz+spl[spl[now].r].siz+spl[now].cnt;
}
inline void zig(int &now)
{//now节点右旋
    int l=spl[now].l;//拎起now的左子树
    spl[now].l=spl[l].r;//l的右子树作为now的左子树
    spl[l].r=now;//now作为原本左儿子的右子树
    now=l;//向上更新编号
    update(spl[now].r),update(now);
}
inline void zag(int &now)
{
    int r = spl[now].r;
    spl[now].r = spl[r].l;
    spl[r].l = now;
    now = r;
    update(spl[now].l),update(now);
}
void splaying(int x,int &y) //我要把x伸展到y那个位置！
{
    if(x==y)
        return;//如果到了终点，return
    int &l=spl[y].l,&r=spl[y].r;//temp
    if(x==l)
        zig(y);//如果左儿子是终点，那就单旋
    else if(x==r)
        zag(y);//右儿子是终点也是单旋
    else//否则就一定是双旋
    {
        if(spl[x].val<spl[y].val)
        {//x在y左子树上
            if(spl[x].val<spl[l].val)// /型
                splaying(x,spl[l].l),zig(y),zig(y);//zigzig情况
            else// <型
                splaying(x,spl[l].r),zag(l),zig(y);//zagzig情况
        }
        else
        {//x在y右子树上
            if(spl[x].val>spl[r].val)// \型
                splaying(x,spl[r].r),zag(y),zag(y);//zagzag情况
            else// >型
                splaying(x,spl[r].l),zig(r),zag(y);//zigzag情况
        }
    }
}
inline void delnode(int now)
{
    splaying(now,root);//将要删的节点移到顶端
    if(spl[now].cnt>1)
        spl[now].siz--,spl[now].cnt--;
    else if(spl[root].r)
    {
        int p=spl[root].r;//右子树
        while(spl[p].l)//找now节点后继
            p=spl[p].l;
        splaying(p,spl[root].r);//将后继移到root右儿子
        spl[p].l=spl[root].l;//root的左子树作为p的左子树
        root=p;//p作为根节点
        update(root);//更新信息
    }
    else//没有后继,直接删除
        root=spl[root].l;
}
void ins(int &now,int &val)
{//插入
    if(!now)//不存在,新建
        newnode(now,val),splaying(now,root);
    else if(val<spl[now].val)//插到左子树上
        ins(spl[now].l,val);
    else if(val>spl[now].val)
        ins(spl[now].r,val);
    else//已存在,cnt++
        spl[now].siz++,spl[now].cnt++,splaying(now,root);
}
void del(int now,int &val)
{
    if(spl[now].val==val)
        delnode(now);
    else if(val<spl[now].val)
        del(spl[now].l,val);
    else
        del(spl[now].r,val);
}
int getrank(int val)
{
    int now=root,rnk=1;
    while(now)
    {
        if(spl[now].val==val)   //找到了要的结点，这个之前的没有
        {
            rnk+=spl[spl[now].l].siz;
            splaying(now,root);
            break;
        }
        if(val<=spl[now].val)
            now=spl[now].l;
        else
        {
            rnk+=spl[spl[now].l].siz+spl[now].cnt;
            now=spl[now].r;
        }
    }
    return rnk;
}
int getnum(int rnk)
{
    int now=root;
    while(now)
    {
        int lsize=spl[spl[now].l].siz;
        if(lsize+1<=rnk&&rnk<=lsize+spl[now].cnt) //如果在这个范围内，那就是当前结点
        {
            splaying(now,root);
            break;
        }
        else if(lsize>=rnk)
            now=spl[now].l;
        else
        {
            rnk-=lsize+spl[now].cnt;
            now=spl[now].r;
        }
    }
    return spl[now].val;
}
signed main(signed argc, char const *argv[])
{
    int n,opt,x;
    cin>>n;
    while(n--)
    {
        cin>>opt>>x;
        if(opt==1)
            ins(root,x);
        else if(opt==2)
            del(root,x);
        else if(opt==3)
            cout<<getrank(x)<<endl;
        else if(opt==4)
            cout<<getnum(x)<<endl;
        else if(opt==5)//前驱
            cout<<getnum(getrank(x)-1)<<endl;
        else//后继
            cout<<getnum(getrank(x+1))<<endl;
    }
    return 0;
}

lzy发过来的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include <cstdio>
#include <iostream> 
using namespace std;
const int N = 1e6 + 5;
int n, m;
struct Splay {
#define rel(x) (x == ch[fa[x]][1])
#define mid ((l + r) / 2)
    int fa[N], ch[N][2], v[N];
    int size[N], root, lazy[N];
    void up(int x) { size[x] = size[ch[x][0]] + size[ch[x][1]] + 1; }
    void rotate(int x) {
        int dad = fa[x], f = rel(x);
        ch[fa[dad]][rel(dad)] = x;
        fa[x] = fa[dad];
        ch[dad][f] = ch[x][f ^ 1];
        fa[ch[x][f ^ 1]] = dad;
        ch[x][f ^ 1] = dad;
        fa[dad] = x;
        up(dad), up(x);
    }
    void splay(int x,int y) {
        for (int f; (f = fa[x]) != y; rotate(x))
            if (fa[f] ^ y)
                rotate(rel(x) == rel(f) ? f : x); 
        root = y ? root : x;
    }
    void build(int bh,int l,int r,int f) {
        if (l > r) return ;
        v[bh] = mid, fa[bh] = f, ch[f][mid > v[f]] = bh;
        build(bh << 1, l, mid-1, bh);
        build(bh << 1 | 1, mid + 1, r, bh);
        up(bh);
    }
    void pushdown(int bh) {
        if(lazy[bh]) {
            swap(ch[bh][0], ch[bh][1]);
            if(ch[bh][0]) lazy[ch[bh][0]] ^= 1;
            if(ch[bh][1]) lazy[ch[bh][1]] ^= 1;
            lazy[bh] = 0;
        }
    }
    int Kth(int bh,int k) {
        pushdown(bh);
        if (size[ch[bh][0]] + 1 == k) return bh;
        if (size[ch[bh][0]] >= k) return Kth(ch[bh][0], k);
        if (size[ch[bh][0]] + 1 < k) return Kth(ch[bh][1], k - size[ch[bh][0]] - 1);
    }
    void change(int l,int r) {
        l = Kth(root, l), r = Kth(root, r + 2);
        splay(l, 0), splay(r, root);
        lazy[ch[r][0]] ^= 1;
    }
    void out(int bh) {
        pushdown(bh);
        if (ch[bh][0]) out(ch[bh][0]);
        if (1 <= v[bh] && v[bh] <= n)
            printf("%d ",v[bh]);
        if (ch[bh][1]) out(ch[bh][1]);
    }
} T;

int main() {
    int x, y;
    scanf("%d%d", &n, &m);
    T.build(1, 0, n + 1, 0), T.root = 1;
    while (m --) scanf("%d%d", &x, &y), T.change(x, y);
    T.out(T.root);
    return 0;
}

这个数据结构可以建立点与点的间接关系与直接关系——可以查询一个点的权值，以及两点是否在同一棵树中，同时对已经连边的两点，切断本来已经有的连边。

$init():$ 用之前先初始化一下，同时注意 $MAXN$ 到底是多少。

$clear():$ 将所有的节点清空。

$haveEdge(x,y):$ 若之前 $x$ 和 $y$ $link()$ 过，则返回 $true$，否则返回 $false$。

$find(x):$ 找到 $x$ 所属树的编号。

$link(x,y):$ 将 $x$ 和 $y$ 连边，前提是 $find(x)!=find(y)$ 。

$cut(x,y):$ 将 $x$ 和 $y$ 之间的边隔断，前提是 $haveEdge(x,y)$ 为 $true$。

一开始赋值的时候给 $sz2[]$ 赋值为初值。

每个操作一次的时间复杂度大概是 $O(logn)$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
struct lctNode
{
    int fa;
    int ch[2];
    //add your info
    int sz,sz2;
    //add your tag
    bool rotatetag;
};
const int MAXN=200000+10;
struct LCT
{
    lctNode nodes[MAXN];
    //the node you can use in the lct
    int n;
    //get a node's kind
    inline int Get(int x)
    {
        return nodes[nodes[x].fa].ch[1] == x;
    }
    //judge a node is the root in the splay tree
    inline bool isRoot(int x)
    {
        return nodes[nodes[x].fa].ch[0] != x && nodes[nodes[x].fa].ch[1] != x;
    }
    //if a node's child tree'struct change,use this to update info
    void pushUp(int x)
    {
        nodes[x].sz = nodes[nodes[x].ch[0]].sz + nodes[nodes[x].ch[1]].sz + nodes[x].sz2 + 1;
    }
    //pushDonw'son function
    void pushRotate(int p)
    {
        if(!p)return;
        swap(nodes[p].ch[0],nodes[p].ch[1]);
        nodes[p].rotatetag^=1;
    }
    //if you need visit a nodes'son,use this to make it real
    void pushDown(int x)
    {
        if(nodes[x].rotatetag)
        {
            pushRotate(nodes[x].ch[0]);
            pushRotate(nodes[x].ch[1]);
            nodes[x].rotatetag = false;
        }
    }
    //if you want ope on node which is unreal,please use it to make it real
    void update(int x)
    {
        if (!isRoot(x))update(nodes[x].fa);
        pushDown(x);
    }
    //rotate x
    void rotate(int x)
    {
        int y=nodes[x].fa;
        int z=nodes[y].fa;
        int k=Get(x);
        if(!isRoot(y)) nodes[z].ch[Get(y)]=x;
        nodes[x].fa=z;
        nodes[nodes[x].ch[!k]].fa=y;
        nodes[y].ch[k]=nodes[x].ch[!k];
        nodes[x].ch[!k]=y;
        nodes[y].fa=x;
        pushUp(y);
        pushUp(x);
        //we don't need to pushUP z,because it's son'stuct change don't produce a change to z
    }
    //splay a node to the splay root
    void splay(int x)
    {
        //before we ope on x,we need make sure it's true
        update(x);
        //rotate twice every route,the first rotate isn't necessary
        for (int p = nodes[x].fa; !isRoot(x); p = nodes[x].fa)
        {
            if (!isRoot(p))rotate(Get(p) == Get(x) ? p : x);
            rotate(x);
        }
    }
    //this function is used to produce a splay from the root in the origin tree to the node x
    //and it will return the splay root
    int Access(int x)
    {
        int p = 0;
        while (x)
        {
            //this cut is on the splay tree so don't cut the edge from son to father
            splay(x);
            //use this to modify the sz2
            nodes[x].sz2+=nodes[nodes[x].ch[1]].sz-nodes[p].sz;
            nodes[x].ch[1] = p;
            //we delete the on son tree of x,so it's necessary to pushUp x
            //use this to modify the sz
            pushUp(x);
            p = x;
            x = nodes[x].fa;
        }
        return p;
    }
    //this function is used to make the node x to the root in the origin tree
    //this function will return a splay tree's root which have node x
    int makeRoot(int x)
    {
        x = Access(x);
        //add a rotate tag to x
        swap(nodes[x].ch[0], nodes[x].ch[1]);
        nodes[x].rotatetag ^= 1;
        return x;
    }
    //this function is used to add a edge between x and y in the origin tree
    //but you need make sure x and y isn't at the same tree
    void link(int x,int y)
    {
        //we must make x to the root else this edge mean the preroot between and y
        x = makeRoot(x);
        makeRoot(y);
        //try optimization it's
        //splay(x);
        nodes[x].fa = y;
        //use this to modify the sz2 of the y
        nodes[y].sz2 += nodes[x].sz;
        while (y)
        {
            pushUp(y);
            y = nodes[y].fa;
        }
    }
    //this function will produce a splay tree from x to y in the origin tree path
    //it will return the splay root,but this root can be not x or y
    int split(int x,int y)
    {
        makeRoot(x);
        return Access(y);
    }
    //this function is used to cut edge x-y
    //but you need make sure there is a edge between x and y
    int res1,res2;
    void cut (int x,int y)
    {
        makeRoot(x);
        Access(y);
        splay(x);
        nodes[y].fa = 0;
        nodes[x].ch[1] = 0;
        pushUp(x);
        res1 = nodes[x].sz;
        res2 = nodes[y].sz;
    }
    //this function is used to find the root in the origin tree
    int find(int x)
    {
        x = Access(x);
        while (nodes[x].ch[0])x = nodes[x].ch[0];
        //if we ope a node in the splay tree,after that make it to the root of the splay
        splay(x);
        return x;
    }
    //this function is used to test if there a edge between x and y
    bool haveEdge(int x,int y)
    {
        if(find(x)==find(y))
        {
            makeRoot(x);
            Access(y);
            splay(x);
            if(nodes[x].ch[1]==y&&nodes[y].ch[0]==0)return true;
        }
        return false;
    }
    //this ope is used to init the LCT
    //please write a empty tree in this place
    //every change on empty tree will useless
    //every use of empty tree will true
    void init()
    {
        nodes[0].fa = 0;
        nodes[0].ch[0] = nodes[0].ch[1] = 0;
        nodes[0].rotatetag = false;
        n = 1;
        //other init ope
        nodes[0].sz=0;
        nodes[0].sz2=0;
    }
    //this function let everynodes be empty tree
    void clear()
    {
        for (int i = 1; i < n; i++)
        {
            nodes[i].rotatetag = false;
            nodes[i].fa = 0;
            nodes[i].ch[0] = nodes[i].ch[1] = 0;
            //other clear operation
 
        }
        n = 1;
    }
    //this function is used to produce a newTree according your info
    int newTree(int _weight)
    {
        //use index: n
        return n++;
    }
    //your special function
} tree;

1044 数树

来源：https://codeforces.com/contest/1277/problem/E

$tag:$ LCT 离散化

题目大意

给出一些有标号的点 $x(1≤x≤10^8)$，共有三种操作：

  1. 将 $u$ 和 $v$ 连起来。
  2. 将 $u$ 和 $v$ 之间的连边删除。
  3. 询问大小不为 $1$ 的树的个数。

输入中可能添加重边，也可能删除不存在的边，略过就好，保证不被忽略的操作 $1$ 不构成环。

题目样例
样例输入
1
2
3
4
5
4
1 1926 817
3
2 817 1926
3
样例输出
1
2
1
0
样例解释

一共有 $4$ 个操作，第一个操作将 $1926$ 和 $817$ 连边，第二个操作询问，输出 $1$ ，第三个操作删除 $1926$ 和 $817$ 的连边，第四个操作询问，输出 $0$。

题目解法

先把询问存起来，离线离散化一波，然后建一棵 $LCT$。$1$ 操作实质上就是 $link$, $2$ 操作实质上就是 $cut$，考虑维护答案 $ans$ 为大小不为 $1$ 的树，则对于操作 $1$：

  1. 若两个大小为 $1$ 的节点 $link$ 一下就会变成一棵大小为 $2$ 的树，所以 $ans++$。
  2. 若两棵大小都不为 $1$，$link$ 一下就会变成一棵大小不为 $1$ 的树，所以 $ans–$。
  3. 若两棵树一棵大小为 $1$ ，一棵不为 $1$ ，则 $link$ 后答案不变。

对于操作 $2$ 同理，对于操作 $3$ 输出 $ans$即可。
时间复杂度 $O(nlogn)$。

完整代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
/*Hatsune Miku 4ever!*/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define _for(i,a,b) for(int i = (a);i < b;i ++)
#define _rep(i,a,b) for(int i = (a);i > b;i --)
#define INF 0x3f3f3f3f3f3f3f3f
#define lowbit(x) ((x)&(-x))
#define pb push_back
#define MIKU 39
#define Design ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define debug() printf("Miku Check OK!\n")
#define bigmiku 3939393939
#define maxn 200039
#define maxe 1000003

struct lctNode
{
    int fa;
    int ch[2];
    //add your info
    int sz,sz2;
    //add your tag
    bool rotatetag;
};

struct G
{
    int n,m;
    int Next[maxe];
    int head[maxn];
    int ver[maxe];
    int tot;
    void clear(int x)
    {
        tot = 0;
        memset(head,0,(x+3)*sizeof(int));
    }
    void add(int x,int y)
    {
        ver[++tot] = y,Next[tot] = head[x],head[x] = tot;
    }
} g;

const int MAXN=200000+10;
struct LCT
{
    lctNode nodes[MAXN];
    //the node you can use in the lct
    int n;

    //get a node's kind
    inline int Get(int x)
    {
        return nodes[nodes[x].fa].ch[1] == x;
    }
    //judge a node is the root in the splay tree
    inline bool isRoot(int x)
    {
        return nodes[nodes[x].fa].ch[0] != x && nodes[nodes[x].fa].ch[1] != x;
    }
    //if a node's child tree'struct change,use this to update info
    void pushUp(int x)
    {
        nodes[x].sz = nodes[nodes[x].ch[0]].sz + nodes[nodes[x].ch[1]].sz + nodes[x].sz2;
    }
    //pushDonw'son function

    void pushRotate(int p)
    {
        if(!p)return;
        swap(nodes[p].ch[0],nodes[p].ch[1]);
        nodes[p].rotatetag^=1;
    }
    //if you need visit a nodes'son,use this to make it real
    void pushDown(int x)
    {
        if(nodes[x].rotatetag)
        {
            pushRotate(nodes[x].ch[0]);
            pushRotate(nodes[x].ch[1]);
            nodes[x].rotatetag = false;
        }
    }
    //if you want ope on node which is unreal,please use it to make it real
    void update(int x)
    {
        if (!isRoot(x))update(nodes[x].fa);
        pushDown(x);
    }
    //rotate x
    void rotate(int x)
    {
        int y=nodes[x].fa;
        int z=nodes[y].fa;
        int k=Get(x);
        if(!isRoot(y)) nodes[z].ch[Get(y)]=x;
        nodes[x].fa=z;
        nodes[nodes[x].ch[!k]].fa=y;
        nodes[y].ch[k]=nodes[x].ch[!k];
        nodes[x].ch[!k]=y;
        nodes[y].fa=x;
        pushUp(y);
        pushUp(x);
        //we don't need to pushUP z,because it's son'stuct change don't produce a change to z
    }
    //splay a node to the splay root
    void splay(int x)
    {
        //before we ope on x,we need make sure it's true
        update(x);
        //rotate twice every route,the first rotate isn't necessary
        for (int p = nodes[x].fa; !isRoot(x); p = nodes[x].fa)
        {
            if (!isRoot(p))rotate(Get(p) == Get(x) ? p : x);
            rotate(x);
        }
    }
    //this function is used to produce a splay from the root in the origin tree to the node x
    //and it will return the splay root
    int Access(int x)
    {
        int p = 0;
        while (x)
        {
            //this cut is on the splay tree so don't cut the edge from son to father
            splay(x);
            //use this to modify the sz2
            nodes[x].sz2+=nodes[nodes[x].ch[1]].sz-nodes[p].sz;
            nodes[x].ch[1] = p;
            //we delete the on son tree of x,so it's necessary to pushUp x
            //use this to modify the sz
            pushUp(x);
            p = x;
            x = nodes[x].fa;
        }
        return p;
    }
    //this function is used to make the node x to the root in the origin tree
    //this function will return a splay tree's root which have node x
    int makeRoot(int x)
    {
        x = Access(x);
        //add a rotate tag to x
        swap(nodes[x].ch[0], nodes[x].ch[1]);
        nodes[x].rotatetag ^= 1;
        return x;
    }
    //this function is used to add a edge between x and y in the origin tree
    //but you need make sure x and y isn't at the same tree
    void link(int x,int y)
    {
        //we must make x to the root else this edge mean the preroot between and y
        x = makeRoot(x);
        makeRoot(y);
        //try optimization it's
        //splay(x);
        nodes[x].fa = y;
        //use this to modify the sz2 of the y
        nodes[y].sz2 += nodes[x].sz;
        while (y)
        {
            pushUp(y);
            y = nodes[y].fa;
        }
    }
    //this function will produce a splay tree from x to y in the origin tree path
    //it will return the splay root,but this root can be not x or y
    int split(int x,int y)
    {
        makeRoot(x);
        return Access(y);
    }
    //this function is used to cut edge x-y
    //but you need make sure there is a edge between x and y
    int res1,res2;
    void cut (int x,int y)
    {
        makeRoot(x);
        Access(y);
        splay(x);
        nodes[y].fa = 0;
        nodes[x].ch[1] = 0;
        pushUp(x);
        res1 = nodes[x].sz;
        res2 = nodes[y].sz;
    }
    //this function is used to find the root in the origin tree
    int find(int x)
    {
        x = Access(x);
        while (nodes[x].ch[0])x = nodes[x].ch[0];
        //if we ope a node in the splay tree,after that make it to the root of the splay
        splay(x);
        return x;
    }
    //this function is used to test if there a edge between x and y
    bool haveEdge(int x,int y)
    {
        if(find(x)==find(y))
        {
            makeRoot(x);
            Access(y);
            splay(x);
            if(nodes[x].ch[1]==y&&nodes[y].ch[0]==0)return true;
        }
        return false;
    }
    //this ope is used to init the LCT
    //please write a empty tree in this place
    //every change on empty tree will useless
    //every use of empty tree will true
    void init()
    {
        nodes[0].fa = 0;
        nodes[0].ch[0] = nodes[0].ch[1] = 0;
        nodes[0].rotatetag = false;
        n = 1;
        //other init ope
        nodes[0].sz=0;
        nodes[0].sz2=0;
    }
    //this function let everynodes be empty tree
    void clear()
    {
        for (int i = 1; i < n; i++)
        {
            nodes[i].rotatetag = false;
            nodes[i].fa = 0;
            nodes[i].ch[0] = nodes[i].ch[1] = 0;
            //other clear operation

        }
        n = 1;
    }
    //this function is used to produce a newTree according your info
    int newTree(int _weight)
    {
        //use index: n
        return n++;
    }
    //your special function

} tree;

int order[maxn];
set<pair<int,int>> eg;
int main()
{

    tree.init();
    int n, m;
    scanf("%d",&n);
    _for(i,1,n+1)
    scanf("%d",&tree.nodes[i].sz2);
    tree.link(1,3);
    tree.link(1,2);
    printf("%d\n",tree.nodes[tree.find(3)].sz);
    return 0;
}

珂朵莉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
struct ChthollyTree
{//迭代器https://www.cnblogs.com/wxquare/p/4699429.html
    ll qmod(ll a,ll b,ll mod){//快速幂
        ll ans=1;
        a=a%mod;
        while(b){
            if(b&1)
                ans=ans*a%mod;
            a=a*a%mod;
            b>>=1;
        }
        return ans;
    }
    struct node
    {
        int l,r;//区间左右端点,[l,r]区间每个数都为val
        mutable ll val;//mutable支持直接在set中修改
        node(int _l,int _r=-1,ll _val=0):
            l(_l),r(_r),val(_val){}
        bool operator <(const node &b)const{
            return l<b.l;
        }
    };
    std::set<node> s;
    void build(ll *a,int n)
    {
        s.clear();
        for(int i=1;i<=n;i++)
            s.insert(node(i,i,a[i]));
        s.insert(node(n+1,n+1,0));
    }
    #define sit std::set<node>::iterator
    sit split(int pos)
    {//将pos所在节点分为[l,pos),[pos,r]两块
        sit it=s.lower_bound(node(pos));
        if(it!=s.end()&&it->l==pos)
            return it;//正好存在,无需分裂
        it--;
        int l=it->l,r=it->r;
        ll val=it->val;
        s.erase(it);
        s.insert(node(l,pos-1,val));
        return s.insert(node(pos,r,val)).first;//insert.first为指向新增元素的迭代器
    }
    inline void assign(int l,int r,ll val)
    {//区间推平
        sit ed=split(r+1),st=split(l);
        s.erase(st,ed);
        s.insert(node(l,r,val));
    }
    inline void update(int l,int r,ll val)
    {//[l,r]加上val
        sit ed=split(r+1);//先找ed,若先找st可能会在找ed的过程中被擦除
        for(sit it=split(l);it!=ed;it++)
            it->val+=val;
    }
    ll kth(int l,int r,int k)
    {//区间第k小
        std::vector<pair<ll,int>>tmp;//数值,数量
        tmp.clear();
        sit ed=split(r+1),st=split(l);
        for(sit it=st;it!=ed;it++)
            tmp.push_back(std::pair<ll,int>(it->val,it->r-it->l+1));
        std::sort(tmp.begin(),tmp.end());
        for(std::vector<std::pair<ll,int>>::iterator it=tmp.begin();it!=tmp.end();++it)
        {
            k-=it->second;
            if(k<=0)
                return it->first;
        }
        return -1;
    }
    ll query(int l,int r,ll k,ll y)
    {//区间k次幂之和取模
        sit ed=split(r+1),st=split(l);
        ll ret=0;
        for(sit it=st;it!=ed;it++)
            ret=(ret+(it->r-it->l+1)*qmod(it->val,k,y))%y;
        return ret;
    }
} ctl;

左偏树

在保持二叉堆基础性质上可以快速合并的堆

定义

外节点：左右儿子不完整的节点

距离：最近的外节点到该点的距离

性质

  1. 节点权值不大于左右儿子权值(堆性质)

  2. 节点左儿子距离≥右儿子距离(左偏性质)

  3. 节点距离=右儿子距离+1

P3377 【模板】左偏树（可并堆）

一开始有 n 个小根堆，每个堆包含且仅包含一个数。接下来需要支持两种操作：

  1. 1 x y：将第 x 个数和第 y 个数所在的小根堆合并（若第 x 或第 y 个数已经被删除或第 x 和第 y 个数在用一个堆内，则无视此操作）。
  2. 2 x：输出第 x 个数所在的堆最小数，并将这个最小数删除（若有多个最小数，优先删除先输入的；若第 x 个数已经被删除，则输出 -1 并无视删除操作）。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
struct LeftistTree
{
    /*
     * 支持如下操作:
     * 合并两个堆 merge,log(p+q)
     * 插入 push ,log(n)
     * 删除最值 pop ,log(n)
     * 删除指定节点 ,log(n)
     * 修改指定节点的值:先删除再加入
     * 取最大/最小值 ,O(1)
     * build复杂度未知,暴建树力建树nlogn
    */
    using type=int;
    int siz=0;
    struct node
    {
        type val;
        int lc,rc,dis,fa;
        node(){}
        node(type val):
            val(val){lc=rc=dis=fa=0;}
    } ltt[maxn];
    #define ls(x) ltt[x].lc
    #define rs(x) ltt[x].rc
    int merge(int x,int y)
    {//x,y为堆顶点元素的编号
        if(x==y)//相同堆不合并
            return x;
        if(!x||!y)//如果有一个为空
            return x+y;//就返回另一个
        if(ltt[x].val>ltt[y].val||(ltt[x].val==ltt[y].val&&x>y))//大根堆
            std::swap(x,y);
        rs(x)=merge(rs(x),y);//往右儿子合并
        ltt[rs(x)].fa=x;
        if(ltt[ls(x)].dis<ltt[rs(x)].dis)
            std::swap(ls(x),rs(x));
        ltt[x].dis=ltt[rs(x)].dis+1;
        return x;//返回新的根编号
    }
    void Merge(int x,int y)
    {//合并x所在堆与y所在堆
        if(ltt[x].val==-1||ltt[y].val==-1)
            return;
        int fx=findfa(x),fy=findfa(y);
        if(fx==fy)
            return;
        ltt[fx].fa=ltt[fy].fa=merge(fx,fy);//维护联通性
    }
    int push(int val,int x)
    {//新加入的点权val,准备加入的堆根编号x
        ltt[++siz].val=val;
        ltt[siz].fa=siz;
        ls(siz)=rs(siz)=ltt[siz].dis=0;
        return merge(siz,x);//当作一棵新树合并到原树上
    }
    int findfa(int x)
    {//获得第x号所在堆的顶点编号
        if(ltt[x].fa!=x)//路径压缩
            return ltt[x].fa=findfa(ltt[x].fa);
        return x;
    }
    type top(int x)
    {//返回x所在堆的顶点的值
        return ltt[findfa(x)].val;
    }
    int pop(int x)
    {//x为当前堆根编号,并且删除x节点
        if(ltt[x].val==-1)//已经被删除
            return -1;
        ltt[x].val=-1;//将节点x标记为删除
        ltt[ls(x)].fa=ls(x);
        ltt[rs(x)].fa=rs(x);//将左右子树合并,并用并查集维护联通
        return ltt[x].fa=merge(ls(x),rs(x));//返回新的根编号
    }
    void del(int x)//待修改,错的
    {//O(logn)删除任意节点,x为节点编号
        int fx=ltt[x].fa,p=merge(ls(x),rs(x));//将左右子树合并
        int &lls=ls(fx),&rrs=rs(x);
        ltt[p].fa=fx;
        if(lls==x)//新子树连接到x原来的父节点
            lls=p;
        else
            rrs=p;
        while(p!=fx)
        {//检查左偏树性质
            if(ltt[lls].dis<ltt[rrs].dis)
                swap(lls,rrs);
            if(ltt[lls].dis==ltt[rrs].dis+1)
                return;
            ltt[fx].dis=ltt[rrs].dis+1;
            p=fx;//向上
            fx=ltt[fx].fa;
            lls=ls(fx);
            rrs=rs(fx);
        }
    }
    int build(int a[],int n)//未验证
    {//将[1,n]的元素全部合并
        ltt[0].dis=-1;
        queue<int>q;
        for(int i=1;i<=n;i++)
        {//处理节点信息
            ltt[i].val=a[i];
            ltt[i].fa=i;
            ls(i)=rs(i)=0;
            q.push(i);
        }
        siz=n;
        while(!q.empty())
        {//队列优化建树
            if(q.size()==1)
                break;
            else{
                int x=q.front();q.pop();
                int y=q.front();q.pop();
                q.push(merge(x,y));
            }
        }
        return q.front();//返回堆根编号
    }
    #undef ls
    #undef rs
} lt;
int a[maxn];
signed main(signed argc, char const *argv[])
{
    int n,m,op,x,y;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        lt.push(a[i],i);
    }
    while(m--)
    {
        cin>>op;
        if(op==1)
        {
            cin>>x>>y;
            lt.Merge(x,y);
        }
        else{
            cin>>x;
            if(lt.ltt[x].val==-1)//被删除
            {
                cout<<-1<<endl;
                continue;
            }
            int f=lt.findfa(x);//所在堆的节点编号
            cout<<lt.ltt[f].val<<endl;
            lt.pop(f);
        }
    }
    return 0;
}
/*
 * 2021-04-20-14.15.43
 * 模板参考:https://www.cnblogs.com/TEoS/p/11351372.html
 * 教程:https://www.bilibili.com/video/BV1eJ411S78v?p=2
*/

P1552 [APIO2012]派遣

在一棵树上，每个点有点权$w$与倍率$l$，有限制$m$，要求一棵子树选择点的点权和不超过$m$。使得子树根节点倍率$l$乘以树上可选择节点数目最大。

思路：枚举每个点作为根，只要在子树中权值最小的点选起使权值之和小于$m$，可以递归地使用堆合并。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
struct LeftistTree
{
    /*
     * 在保持二叉堆基础性质上可以快速合并的堆
     * 外节点:左右儿子不完整的节点
     * 距离:最近的外节点到该点的距离
     * 性质:
     * 1.节点权值不大于左右儿子权值(堆性质)
     * 2.节点左儿子距离≥右儿子距离(左偏性质)
     * 3.节点距离=右儿子距离+1
     * 支持如下操作:
     * 合并两个堆 merge,log(p+q)
     * 插入 push ,log(n)
     * 删除最值 pop ,log(n)
     * 删除指定节点 ,log(n)
     * 修改指定节点的值:先删除再加入
     * 取最大/最小值 ,O(1)
     * lt.sum[lt.findfa(x)],可以得到x所在堆的元素和
     * lt.cnt[lt.findfa(x)],可以得到x所在堆的大小
     * build可快速建树,暴建树力建树nlogn
    */
    using type=int;
    int siz=0;
    struct node
    {
        type val;
        int lc,rc,dis,fa;
        node(){}
        node(type val):
            val(val){lc=rc=dis=fa=0;}
    } ltt[maxn];
    type sum[maxn];//堆中元素之和
    int cnt[maxn];//每一个堆的大小
    #define ls(x) ltt[x].lc
    #define rs(x) ltt[x].rc
    inline void update(int x)
    {
        sum[x]=sum[ls(x)]+sum[rs(x)]+ltt[x].val;//更新堆中元素和
//        printf("node[%d],l=%d,r=%d\n",x,ls(x),rs(x));
        cnt[x]=cnt[ls(x)]+cnt[rs(x)]+1;
        if(ltt[ls(x)].val==-1)
        {
            sum[x]-=sum[ls(x)];
            cnt[x]-=cnt[ls(x)];
        }
//        printf("cnt[%d]=%d+%d+1=%d\n",x,cnt[ls(x)],cnt[rs(x)],cnt[x]);
//        printf("sum[%d]=%d=%d+%d+%d\n\n",x,sum[x],sum[ls(x)],sum[rs(x)],ltt[x].val);
    }
    int merge(int x,int y)
    {//x,y为堆顶点元素的编号
        if(x==y)//相同堆不合并
            return x;
//        printf("%d,%d\n",x,y);
        if(!x||!y)//如果有一个为空
            return x+y;//就返回另一个
        if(ltt[x].val>ltt[y].val||(ltt[x].val==ltt[y].val&&x>y))//大根堆
            std::swap(x,y);
//        printf("%d:ls=%d,rs=%d\n",x,ls(x),rs(x));
        rs(x)=merge(rs(x),y);//往右儿子合并
        ltt[rs(x)].fa=x;
        update(x);//回溯更新新树信息
        if(ltt[ls(x)].dis<ltt[rs(x)].dis)
            std::swap(ls(x),rs(x));
        ltt[x].dis=ltt[rs(x)].dis+1;
        return x;//返回新的根编号
    }
    void Merge(int x,int y)
    {//合并x所在堆与y所在堆
        if(ltt[x].val==-1||ltt[y].val==-1)//根据需要注释
            return;
        int fx=findfa(x),fy=findfa(y);
        if(fx==fy)
            return;
        ltt[fx].fa=ltt[fy].fa=merge(fx,fy);//维护联通性
    }
    int push(int val,int x)
    {//新加入的点权val,准备加入的堆根编号x
        ltt[++siz].val=val;
        ltt[siz].fa=siz;
        ls(siz)=rs(siz)=ltt[siz].dis=0;
        cnt[siz]=1;
        sum[siz]=ltt[siz].val;
        return merge(siz,x);//当作一棵新树合并到原树上
    }
    int findfa(int x)
    {//获得第x号所在堆的顶点编号
        if(ltt[x].fa!=x)//路径压缩
            return ltt[x].fa=findfa(ltt[x].fa);
        return x;
    }
    type top(int x)
    {//返回x所在堆的顶点的值
        return ltt[findfa(x)].val;
    }
    int pop(int x)
    {//x为当前堆根编号,并且删除x节点
        if(ltt[x].val==-1)//已经被删除
            return -1;
        ltt[x].val=-1;//将节点x标记为删除
        ltt[ls(x)].fa=ls(x);
        ltt[rs(x)].fa=rs(x);//将左右子树合并
        return ltt[x].fa=merge(ls(x),rs(x));//返回新的根编号,并查集维护联通
    }
    void del(int x)//有问题,待修改
    {//O(logn)删除任意节点,x为节点编号
        ltt[x].val=-1;//标记删除
        ltt[ls(x)].fa=ls(x);
        ltt[rs(x)].fa=rs(x);//先将左右子树拆出来
        int fx=ltt[x].fa,p=merge(ls(x),rs(x));//将左右子树合并
        int &lls=ls(fx),&rrs=rs(x);
        ltt[x].fa=p;
        if(lls==x)//新子树连接到x原来的父节点
            lls=p;
        else
            rrs=p;
        while(p!=fx)
        {//检查左偏树性质
            if(ltt[lls].dis<ltt[rrs].dis)
                swap(lls,rrs);
            if(ltt[lls].dis==ltt[rrs].dis+1)
                return;
            ltt[fx].dis=ltt[rrs].dis+1;
            p=fx;//向上
            fx=ltt[fx].fa;
            lls=ls(fx);
            rrs=rs(fx);
        }
    }
    int build(int a[],int n)//未验证
    {//将[1,n]的元素全部合并
        ltt[0].dis=-1;//空节点默认距离为-1
        queue<int>q;
        for(int i=1;i<=n;i++)
        {//处理节点信息
            ltt[i].val=a[i];
            ltt[i].fa=i;
            ls(i)=rs(i)=0;
            q.push(i);
        }
        siz=n;
        while(!q.empty())
        {//队列优化建树
            if(q.size()==1)
                break;
            else{
                int x=q.front();q.pop();
                int y=q.front();q.pop();
                q.push(merge(x,y));
            }
        }
        return q.front();//返回堆根编号
    }
    #undef ls
    #undef rs
} lt;
int a[maxn],b[maxn],c[maxn],l[maxn];
int ans=0,m,cnt[maxn];
vector<int>G[maxn];
void dfs(int x)
{
    for(int &v:G[x])
    {
        dfs(v);
        lt.Merge(x,v);//合并子树
    }
    while(lt.sum[lt.findfa(x)]>m)//控制堆的元素和
        lt.pop(lt.findfa(x));
    ans=max(ans,l[x]*lt.cnt[lt.findfa(x)]);
}
signed main(signed argc, char const *argv[])
{
    #endif
    int n;
    cin>>n>>m;//个数,预算
    for(int i=1;i<=n;i++)
    {
        cin>>b[i]>>c[i]>>l[i];
        G[b[i]].push_back(i);
        lt.push(c[i],i);
    }
    dfs(1);
    cout<<ans<<endl;
    return 0;
}
/*
 * 2021-04-20-14.15.43
 * 每个忍者都有一个上级,形成一个树形结构
 * 满意度=管理者领导力水平
 * dp[x]=l[x]*cnt,cnt为x子树上权值和不超过m的最大数量
 * 使用大根堆,不断弹栈来保证总和<=m
 */

ST表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
const int maxn=100005;
int a[maxn],d[maxn][20],lg[maxn];
void init(int n)
{//d[i][j]表示以i为起点,2^j长度的最值
    for(int i=1;i<=n;i++){
        lg[i]=lg[i-1]+((1<<(lg[i-1]+1))==i);
        d[i][0]=a[i];
    }
    for(int j=1;(1<<j)<=n;j++)//枚举长度
        for(int i=1;i+(1<<j)-1<=n;i++)//枚举起点,倍增+DP
            d[i][j]=max(d[i][j-1],d[i+(1<<(j-1))][j-1]);
}
int rmq(int l,int r)
{
    int k=lg[r-l+1];
    return max(d[l][k],d[r-(1<<k)+1][k]);
}
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int n,m;//长度与询问个数
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    init(n);
    while(m--)
    {
        int l,r;
        scanf("%d%d",&l,&r);
        printf("%d\n",rmq(l,r));
    }
    return 0;
}

分块

区间众数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
const int maxn=40005,lim=205,inf=0x3f3f3f3f;
int a[maxn],c[maxn],id=0,f[lim][lim];
int siz,num,belong[maxn];
struct block
{
    int l,r;
} b[lim];
map<int,int> QAQ;
vector<int> pos[maxn];//存储种类下标
int val[maxn];//QAQ的反函数
void build(int n)
{
    siz=sqrt(n);
    num=n/siz;
    if(n%siz)
        num++;
    for(int i=1;i<=num;i++)
        b[i].l=(i-1)*siz+1,b[i].r=i*siz;
    b[num].r=n;//特殊处理
    for(int i=1;i<=n;i++)
        belong[i]=(i-1)/siz+1;
    for(int i=1;i<=n;i++)
    {
        if(QAQ[a[i]]==0)
        {
            QAQ[a[i]]=++id;//新编号
            val[id]=a[i];
        }
        a[i]=QAQ[a[i]];
        pos[a[i]].push_back(i);//记录出现位置,自动升序
    }
    //暴力预处理区间众数,f[i][j]表示i块到j块*众数编号*
    for(int i=1;i<=belong[n];i++)
    {
        memset(c,0,sizeof(c));
        int maxc=0,ans=0;
        for(int j=b[i].l;j<=n;j++)//枚举起点,一直处理到最后
        {
            c[a[j]]++;//统计数量
            if(c[a[j]]>maxc||c[a[j]]==maxc&&val[a[j]]<val[ans])
            {//更新当前众数答案
                maxc=c[a[j]];//更新众数数量
                ans=a[j];
            }
            f[i][belong[j]]=ans;
        }
    }
}
int querynum(int l,int r,int x)//查询[l,r]内编号为x的数量
{
    return upper_bound(pos[x].begin(),pos[x].end(),r)-lower_bound(pos[x].begin(),pos[x].end(),l);
}
int query(int l,int r)
{
    int ans=0,maxc=0;
    ans=f[belong[l]+1][belong[r]-1];//提溜出来中间的整块众数
    maxc=querynum(l,r,ans);
    if(belong[l]==belong[r])
    {
        for(int i=l;i<=r;i++)
        {
            int num=querynum(l,r,a[i]);//查询a[i]在[l,r]上的个数
            if(num>maxc||num==maxc&&val[a[i]]<val[ans])
            {
                ans=a[i];
                maxc=num;
            }
        }
        return val[ans];
    }
    //不在同一块
    for(int i=l;i<=b[belong[l]].r;i++)//枚举左面散装
    {
        int num=querynum(l,r,a[i]);//查询a[i]在[l,r]上的个数
        if(num>maxc||num==maxc&&val[a[i]]<val[ans])
        {
            ans=a[i];
            maxc=num;
        }
    }
    for(int i=b[belong[r]].l;i<=r;i++)
    {
        int num=querynum(l,r,a[i]);//查询a[i]在[l,r]上的个数
        if(num>maxc||num==maxc&&val[a[i]]<val[ans])
        {
            ans=a[i];
            maxc=num;
        }
    }
    return val[ans];//返回实际种类
}
signed main()
{
    int n,m,ans=0;//n株蒲公英,m次询问
    n=read(),m=read();
    for(int i=1;i<=n;i++)
        a[i]=read();
    build(n);
    while(m--)
    {//强行在线,输出出现次数最多的数
        int l0,r0,l,r;
        l0=read(),r0=read();
        l=(l0+ans-1)%n+1;
        r=(r0+ans-1)%n+1;
        if(l>r)//强行在线...
            swap(l,r);
        ans=query(l,r);
        printf("%d\n",ans);
    }
    return 0;
}

莫队

时刻注意桶是否越界。

例题

CF86D Powerful

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
struct block
{
    int l,r,id;
}Q[maxn];
int a[maxn],pos[maxn];
ll ans[maxn],c[maxn*5],res;
void add(int x)
{//
    res-=c[a[x]]*c[a[x]]*a[x];
    c[a[x]]++;
    res+=c[a[x]]*c[a[x]]*a[x];
}
void del(int x)
{
    res-=c[a[x]]*c[a[x]]*a[x];
    c[a[x]]--;
    res+=c[a[x]]*c[a[x]]*a[x];
}
signed main(signed argc, char const *argv[])
{
    int n,q;
    cin>>n>>q;
    int siz=sqrt(n);
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        pos[i]=i/siz;
    }
    for(int i=1;i<=q;i++)
        cin>>Q[i].l>>Q[i].r,Q[i].id=i;
    sort(Q+1,Q+q+1,[](const block &x,const block &y){
            return pos[x.l]==pos[y.l]?x.r<y.r:pos[x.l]<pos[y.l];
        });
    int l=1,r=0;
    for(int i=1;i<=q;i++)
    {
        while(l<Q[i].l)
            del(l++);
        while(l>Q[i].l)
            add(--l);
        while(r<Q[i].r)
            add(++r);
        while(r>Q[i].r)
            del(r--);
        ans[Q[i].id]=res;
    }
    for(int i=1;i<=q;i++)
        cout<<ans[i]<<'\n';
    return 0;
}
/*
 *2021-04-02-21.24.26
 *[l,r]区间询问,输出权值*出现次数的平方的和
*/