数论与组合数学

发表于 更新于 分类于 阅读次数：

这里记录了数学方面平时个人常用的代码模板。

数学

和式 公式
$S_k=\sum\limits_{i=1}^{n}i^k$ $S_k=\dfrac{(n+1)^{k+1}-1-C_{k+1}^{2}S_{k-1}-C_{k+1}^{3}S_{k-2}-\dots-C_{k+1}^{k}S_{1}-n}{C_{k+1}^{1}}$
$S_2=\sum\limits_{i=1}^{n}i^2$ $S_2=\dfrac{n(n+1)(2n+1)}{6}$
$\sum\limits_{i=1}^{n}(2i-1)^2$ $\dfrac{n\times(4n^2-1)}{3}$
$\sum\limits_{i=1}^{n}i(i+1)$ $\dfrac{n(n+1)(n+2)}{3}$
$S_3=\sum\limits_{i=1}^{n}i^3$ $S_3=(\dfrac{n\times (n+1)}{2})^2$
$\sum\limits_{i=1}^{n}(2i-1)^3$ $n^2(2n^2-1)$
$\sum\limits_{i=1}^{n}i(i+1)(i+2)$ $\frac{n(n+1)(n+2)(n+3)}{4}$
$S_4=\sum\limits_{i=1}^{n}i^4$ $\dfrac{n(n+1)(2n+1)(3n^2+3n+1)}{30}$
$\sum\limits_{i=1}^{n}i(i+1)(i+2)(i+3)$ $\dfrac{n(n+1)(n+2)(n+3)(n+4)}{5}$
$S_5=\sum\limits_{i=1}^{n}i^5$ $\dfrac{n^2(n+1)^2(2n^2+2n-1)}{12}$

常见组合数公式

  • $C_n^m=\dfrac{n!}{m!(n-m)!}$
  • $C_n^m=C_{n-1}^{m-1}+C_{n-1}^m$
  • $mC_n^m=nC_{n-1}^{m-1}$
  • $C_n^0+C_n^1+C_n^2+\dots+C_n^n=2^n$
  • $C_n^0+C_n^2+C_n^4+\dots=C_n^1+C_n^3+C_n^5+\dots=2^{n-1}$
  • $C_n^n+C_{n+1}^n+C_{n+2}^n+\dots+C_{n+m}^n=C_{n+m+1}^{n+1}$
  • $1C_n^1+2C_n^2+3C_n^3+\dots+nC_n^n=n2^{n-1}$
  • $1^2C_n^1+2^2C_n^2+3^2C_n^3+\dots+n^2C_n^n=n(n+1)2^{n-2}$
  • $(C_n^0)^2+(C_n^1)^2+(C_n^2)^2+\dots+(C_n^n)^2=C_{2n}^n$

快速幂

时间复杂度$O(logn)$

1
2
3
4
5
6
7
8
9
10
11
12
ll qmod(ll a,ll b,ll mod)  //快速幂
{
    ll ans=1;
    a=a%mod;
    while(b){
        if(b&1)
            ans=ans*a%mod;
        a=a*a%mod;
        b>>=1;
    }
    return ans;
}

防爆快速幂

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
ull mul_mod(ull x,ull n,ull mod)
{
    x%=mod,n%=mod;
    ull ret=0;
    while(n){
        if(n&1){
            ret+=x;
            if(ret>=mod)
                ret-=mod;
        }
        x<<=1;
        if(x>=mod)
            x-=mod;
        n>>=1;
    }
    return ret;
}
ull qmod(ull a,ull b)
{
    ull ans=1;
    while(b){
        if(b&1)
            ans=mul_mod(ans,a,mod);
        a=mul_mod(a,a,mod);
        b>>=1;
    }
    return ans;
}

超级快速幂

详情移步欧拉定理
$$
a^{b^c}%\ p=a^{b^c%(p-1)}%\ p
$$

1
2
ll rem = qmod(b,c,mod-1);
ll ans = qmod(a,rem,mod);//a必须与mod互质

乘法逆元

附：费马小定理：若$p$是质数，且$a$、$p$互质，那么$a^{p-1} \equiv 1\pmod p$。
$$
{\color{green} \frac{a}{c} mod\ p =a * c ^ {\ p-2} mod \ p}
$$

1
2
3
4
ll inv(ll a,ll p)
{//求a在模p下的乘法逆元（p是素数）
    return qmod(a,p-2,p);//qmod在上面
}

扩展欧几里得求逆元

1
2
3
4
5
6
ll inv1(ll a,ll mod)//扩展欧几里得求逆元
{//mod可为非素数
    ll x,y;
    exgcd(a,mod,x,y);
    return (x%mod+mod)%mod;//防止出现负数的情况
}

组合数取模

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
const int MOD = 1E9+7;
const int N = 100000+5;
ll fac[N],inve[N];//fac为阶乘,inve为1~n的所有逆元
void init(){
    fac[0]=fac[1]=inve[0]=inve[1]=1;
    for(ll i=2; i<N; i++) {
        fac[i]=fac[i-1]*i%MOD;
        inve[i]=(MOD-MOD/i)*inve[MOD%i]%MOD;
    }
    for(ll i=1; i<N; i++)
        inve[i]=inve[i]*inve[i-1]%MOD;
}
ll C(ll n,ll m,ll p)
{//组合数C(n,m)取模p(p是素数)
    if(n<0 || m<0 || m>n) return 0;
    if(n==m) return 1;
    return fac[n]*inve[m]%p*inve[n-m]%p;
}

zzl的组合数模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
ll fac[maxn],inv[maxn],a[maxn];
ll quick(ll a,ll b){//快速幂
    ll ans=1;
    while(b){
        if(b&1)ans=ans*a%mod;
        a=a*a%mod;
        b/=2;
    }
    return ans%mod;
}
ll ccc(ll n,ll m){//求组合数C(n,m)=n!/m!(n-m)!
    if(n<0 || m<0 || m>n) return 0;
    if(n==m) return 1;
    return fac[n]*inv[m]%mod*inv[n-m]%mod;
//    return (fac[n] * quick(fac[m], mod - 2) % mod * quick(fac[n - m], mod - 2) % mod)%mod;
}
void initccc(ll n)
{
    fac[0] = 1;
    for (int i = 1; i <= n ;i++){
        fac[i] = fac[i - 1] * i % mod;
    }
    inv[n]=quick(fac[n],mod-2);
    for(int i=n-1;i>=1;i--)
        inv[i]=inv[i+1]*(i+1ll)%mod;
}

Lucas

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
ll POW(ll a,ll b,ll p)
{
    ll ans = 1;
    while(b){
        if(b&1)
            ans = (ans%p*a%p) % p;
        a = (a%p*a%p) % p;
        b >>= 1;
    }
    return ans%p;
}
ll C(ll n,ll m,ll p)
{
    if(m > n)return 0;
    if(m == n)return 1;
    if(m > n - m)m = n - m;
    ll a = 1, b = 1 ;
    for(ll i = 0 ; i < m ; i++){
        a = a * (n - i) % p;
        b = b * (i + 1) % p;
    }
    return a * POW(b,p-2,p) % p;
}
ll lucas(ll n,ll m,ll p){//C(n,m)%p
    if(m == 0)
        return 1;
    return C(n%p,m%Wp,p)*lucas(n/p,m/p,p)%p;
}

KuangBin的素数筛

素数筛选，存在小于等于 $MAXN$ 的素数
$prime[0]$ 存的是素数的个数，$prime[i] $存的是第$i$个素数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
const int MAXN=10000;
int prime[MAXN+1];
void getPrime()
{
    memset(prime,0,sizeof(prime));
    for(int i=2;i<=MAXN;i++)
    {
        if(!prime[i])prime[++prime[0]]=i;
        for(int j=1;j<=prime[0]&&prime[j]<=MAXN/i;j++)
        {
            prime[prime[j]*i]=1;
            if(i%prime[j]==0) break;
        }
    }
}

欧拉筛

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
const int MAXN=100010;
int phi[MAXN+1],prime[MAXN+1],psize;//psize是素数的个数,prime[i]存着第i个素数
bool isprime[MAXN+1];
void getlist(void)
{
    memset(isprime,1,sizeof(isprime));
    psize=0;
    isprime[1]=false;
    phi[1]=1;
    for(int i=2;i<=MAXN;i++){
        if(isprime[i])
            prime[++psize]=i,phi[i]=i-1;
        for(int j=1;j<=psize&&i*prime[j]<=MAXN;j++){
            isprime[i*prime[j]]=false;
            if(i%prime[j]==0)
            {
                phi[i*prime[j]]=phi[i]*prime[j];
                break;
            }
            phi[i*prime[j]]=phi[i]*(prime[j]-1);
        }
    }
}

LCM

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
long long gcd(long long a,long long b)
{
    if(a<b)
        swap(a,b);
    long long r;
    while((r=a%b)){
        a=b;
        b=r;
    }
    return b;
}
long long lcm(long long a,long long b)
{
    return (a*b)/gcd(a,b);
}

线性同余

线性同余:对于方程$ax\equiv c\pmod{b}$，即$\ ax+by=c$
若题意可列出未知数为$x$的方程 $(m+ax)%b=n$ => $ax=(n-m)%b$ => $ax+by=n-m $，$\ a、b、n、m$为已知常数，$x、y$为未知数，代入exgcd求得$x_0$

扩展欧几里得算法在求$a,b$的最大公约数同时,求出特殊的裴蜀等式$ax+by=gcd(a,b)$的一组特解
对方程$ax+by=c$，若$c%gcd(a,b)!=0$，即$c$不是gcd的整数倍,则无解
即$ax + by = c $有整数解时当且仅当$c$是$gcd(a,b)$的倍数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
ll exgcd(ll a,ll b,ll &x,ll &y)//扩展欧几里得,要保证a>b
{//传递x,y的引用
    if(b == 0)
    {//推理1，终止条件
        x = 1;
        y = 0;
        return a;//找到gcd,一路返回上去
    }
    ll r = exgcd(b, a%b, x, y);
    //先得到更底层的x2,y2,再根据计算好的x2,y2计算x1，y1。
    //推理2，递推关系x1=y2,y1=x2-(a/b)*y2;
    ll t = y;
    y = x - (a/b) * y;//(a/b)向下取整
    x = t;
//    printf("x1=%d,y1=%d,r=%d\n",x,y,r);
    return r;
}

通解$\ x=(\frac{c}{gcd(a,b)} ) \times x_0+\frac{b}{gcd(a,b)}\times t $，$x_0$为一特解

$\ y=(\frac{c}{gcd(a,b)} ) \times y_0+\frac{a}{gcd(a,b)}\times t$
($x_0\ , y_0$ 为方程的一组特解， $t$为整数)

推荐这篇https://blog.csdn.net/yoer77/article/details/69568676

https://blog.csdn.net/baidu_33153085/article/details/52137179#commentBox

最小正整数解结论证明:https://www.cnblogs.com/hadilo/p/5914302.html第四部分

$ax+by=c$最小解正整数解$\
x=\left( \left(\frac{c}{gcd}\times x_0 \mod \frac{b}{gcd}\right)+\frac{b}{gcd}\right)\mod \frac{b}{gcd}$

例题CF1500B - Two chandeliers

题意

两盏灯笼进行周期性闪烁，一个周期为$n$，一个周期为$m$，数组中每个数字保证不同，输出第$k$次不同是哪一天。

思路

https://www.cnblogs.com/ztns/p/14545229.html

一个循环节的长度为$lcm(n,m)$，可以考虑一个循环节中老板。

第$x$天$a$移到$i$位，$b$移到$j$位，则$\begin{cases}i=x \mod n \ j=x \mod m\end{cases}$，若老板不生气则说明$a_i=b_j$.

对以上式子可得$\begin{cases} x=i+k_1\times n \ x=j+ k_2 \times m\end{cases}$，合并得$k_1\times n-k_2\times m=j-i$，注意若$gcd(n,m)\nmid (j-i)$则是无解的，该颜色的灯笼永远不会相同.

可以使用$exgcd$得到一组解$k_1,k_2$，将其中一个——此处选择$k_1$变为最小正整数解代入$x=i+k_1\times n$即可求得时间点$x$，则在$lcm(n,m)$周期中，时间点$x$时老板是不生气的，且对于这个颜色，只有此时是不生气的。

将这些老板不生气的时间点存起来，一个循环节内老板生气时间便可求出，并且在最后一轮进行二分时间即可求得答案。

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
ll exgcd(ll a,ll b,ll &x,ll &y)//扩展欧几里得,要保证a>b
{//传递x,y的引用
    if(b == 0)
    {//推理1，终止条件
        x = 1;
        y = 0;
        return a;//找到gcd,一路返回上去
    }
    ll r = exgcd(b, a%b, x, y);
    //先得到更底层的x2,y2,再根据计算好的x2,y2计算x1，y1。
    //推理2，递推关系x1=y2,y1=x2-(a/b)*y2;
    ll t = y;
    y = x - (a/b) * y;//(a/b)向下取整
    x = t;
    return r;
}
int mp[maxn],a[maxn],b[maxn];
vector<int>rec;
signed main(signed argc, char const *argv[])
{
    int n,m,k;
    cin>>n>>m>>k;
    int g=gcd(n,m),L=lcm(n,m);
    for(int i=1;i<=n;i++)
        cin>>a[i],mp[a[i]]=i;
    for(int i=1;i<=m;i++)
    {
        cin>>b[i];
        if(mp[b[i]]==0)
            continue;
        int c=i-mp[b[i]];
        if(c%g)
            continue;
        ll k1,k2;
        exgcd(n,m,k1,k2);
        k1=((c/g*k1%(m/g))+(m/g))%(m/g);//最小正整数解
        rec.push_back(mp[b[i]]+k1*n);
    }
    sort(rec.begin(),rec.end());
    int val=rec.size();//多少个相同
    int ans=k/(L-val),ret=k-ans*(L-val),ans2=INF;
    if(k%(L-val)==0)
    {//最后一轮可能没必要跑满
        ans--;
        ret+=L-val;
    }
    int l=0,r=L;
    while(l<=r)//二分最后一轮满足ret需要多少天
    {
        int mid=(l+r)>>1;
        int now=upper_bound(rec.begin(),rec.end(),mid)-rec.begin();//[1,mid]范围内相同天数
        if(mid-now>=ret)//mid-now即为该部分的贡献
        {//多了,但是满足
            r=mid-1;
            ans2=min(ans2,mid);
        }
        else
            l=mid+1;
    }
    cout<<ans*L+ans2<<endl;
    return 0;
}

中国剩余定理（CRT）

求解形式如下一元线性同余方程组，其中$n_1,n_2,\dots,n_k$两两互质

$\begin{cases}x\equiv a_1\pmod{n_1}\x\equiv a_2\pmod{n_2}\ \dots \x\equiv a_n\pmod{n_k}\end{cases}$

扩展CRT

扩展CRT与普通的CRT区别在于模数可以不互质。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include<bits/stdc++.h>
#define For(i, a, b) for(register int i = a; i <= b; ++ i)
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 10;
ll n, a[maxn], b[maxn]; 
ll nowa = 1, nowb;
ll mul(ll a, ll b, ll mod)
{
    ll res = 0, f = 1;
    if(b < 0) f = -1, b *= f;
    while(b)
    {
        if(b & 1)
            (res += a) %= mod;
        b >>= 1, (a <<= 1) %= mod;
    }
    return res * f;
}
ll ex_gcd(ll a, ll &x, ll b, ll &y) {
    if(b == 0) {
        x = 1, y = 0;
        return a;
    }
    ll tmp = ex_gcd(b, x, a % b, y);
    ll xx = y, yy = x - a / b * y;
    x = xx, y = yy;
    return tmp;
}
int main() {
    ll x, y;
    scanf("%lld", &n);
    For(i, 1, n) {
        scanf("%lld%lld", &a[i], &b[i]);
        ll gcd = ex_gcd(nowa, x, a[i], y);
        x = (mul(x, (b[i] - nowb) / gcd, a[i] / gcd) + a[i] / gcd) % (a[i] / gcd);
        nowb = nowa * x + nowb;
        nowa = nowa / gcd * a[i];
        nowb = (nowb % nowa + nowa) % nowa;
    }
    printf("%lld\n", nowb);
    return 0;
}

整除分块

$O(\sqrt{n})$时间内计算$\sum\limits_{i=1}^n\lfloor\dfrac{n}{i} \rfloor$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include<bits/stdc++.h>
using namespace std;
int main()
{
    int n,ans=0;
    cin>>n;
    for(int l=1,r=1;l<=n;l=r+1)//l为区间左端点,r为右端点
    {
        r=n/(n/l);
        ans+=(r-l+1)*(n/l);//这个区间所有的值都为(n/l)向下取整
    }
    cout<<ans<<endl;
    return 0;
}

矩阵快速幂(MFP)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
const ll maxn=105,mod=1000000007;
struct Matrix
{
    ll a[maxn][maxn],r,c;
    Matrix(){}
    Matrix(const Matrix &m)
    {
        this->r=m.r;
        this->c=m.c;
        for(int i=1;i<=m.r;i++)
            for(int j=1;j<=m.c;j++)
                a[i][j]=m.a[i][j];
    }
    Matrix (ll row,ll col):
        r(row),c(col){memset(a,0,sizeof(a));}
};
ostream &operator << (ostream &os,const Matrix m)
{
    for(int i=1;i<=m.r;i++)
    {
        for(int j=1;j<=m.c;j++)
        {
            cout<<m.a[i][j]<<' ';
        }
        cout<<'\n';
    }
    return os;
}
Matrix operator *(const Matrix &m1,const Matrix &m2)
{//矩阵相乘
    Matrix ret(m1.r,m2.c);
    for(int i=1;i<=m1.r;i++)
        for(int k=1;k<=m1.c;k++)
            for(int j=1;j<=m2.c;j++)
                ret.a[i][j]=(ret.a[i][j]+(m1.a[i][k]*m2.a[k][j])%mod)%mod;
    return ret;
}
Matrix operator^(Matrix m,ll k)
{//矩阵m的k次幂
    Matrix ret(m);//重载乘法后和，快速幂一样的...
    k--;
    while(k)
    {
//        cout<<k<<":\nret:\n"<<ret<<"m:\n"<<m<<endl;
        if(k&1)
            ret=ret*m;
        m=m*m;
        k>>=1;
    }
    return ret;
}

逆序数

  • 逆序：排列中前后位置与大小顺序相反的一对数

  • 逆序数：排列中逆序的总数

O(nlogn)​求法

  • 法1：使用归并排序

  • 法2：使用树状数组优化，注意使用前将c数组清空。

1
2
3
4
5
6
7
discre(n);//数据过大需要离散化
ll ans=0;
for(int i=n;i;i--){
    ans+=query(a[i]-1);
    update(a[i],1,n);
}
cout<<ans<<endl;//逆序数

应用

  • 隧道超车问题
  • 冒泡排序的交换次数

康托展开

当前排列在n个不同元素的全排列中的名次
$$
{\color{green}ans=\sum_{i=1}^n \ k_i \times (n-i)!}
$$

$ans+1$即为给出排列在全排列的名次，为给出排列第$i$位$a_i$,其后比$a_i$小的个数。

遍历统计$k_i$时间复杂度$O(n^2)$，内层循环改用树状数组统计，时间复杂度降为$O(nlogn)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
const int mod=998244353;
const int maxn=1000005;
ll a[maxn],fac[maxn]={1,1,2,6},c[maxn];
#define lowbit(x) (x&(-x))
void add(int k,ll num,int n)
{
    while(k<=n){
        c[k]+=num;
        k+=lowbit(k);
    }
}
ll query(int k)
{
    ll sum=0;
    while(k){
        sum+=c[k];
        k-=lowbit(k);
    }
    return sum;
}
ll contor(ll arr[],int n)
{
    ll ans=0;
    for(int i=1;i<=n;i++){
        ll cnt=query(a[i]-1);//查询a[i]前面有多少个1,即比a[i]小还没有用过的数字个数
        add(a[i],-1,n);//遇到一个点则修改该点为0
        ans+=(cnt*fac[n-i])%mod;//计算第i位*小于*a[i]有多少个组合
        ans%=mod;
    }
    return (ans+1)%mod;
}
void init(int n)
{
    for(int i=4;i<=n;i++)//阶乘前缀积
        fac[i]=(fac[i-1]*i)%mod;
    for(int i=1;i<=n;i++)
        add(i,1,n);//所有点都修改为1
}

牛顿迭代法

牛顿迭代法（Newton’s method）又称为牛顿-拉夫逊（拉弗森）方法（Newton-Raphson method），它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。

使用牛顿迭代法求解方程相当于使用函数$f(x)$的泰勒级数的前面几项来寻找方程$f(x)=0$的根。

原理：通过切线不断逼近

img

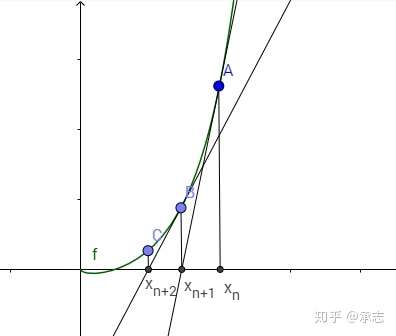
在上图当中，我们要求$f(x)$的根，我们先找到了一个$x_n$点，我们在$f(x_n)$处进行求导取得了它的切线。显然只要这个切线的斜率不为$0$，那么我们一定可以获得它和$x$轴的交点。我们将这个交点作为下一个取值，也就是的$x_{n+1}$点。我们重复上述过程进行迭代，很快就可以得到一个足够接近的解。

过点$(x_n,f(x_n))$的切线，斜率为$f’(x_n)$，截距$b=f(x_n)-f’(x_n)x_n$，方程即为$y=f’(x_n)x+f(x_n)-f’(x_n)x_n$。

令$x=x_{n+1},y=0$可以求得该方程与$x$轴的交点$x_{n+1}=x_n-\dfrac{f(x_n)}{f’(x_n)}$。

当迭代结果与上一次的迭代结果相同或者小于一定阈值时，本次的结果即为函数的根。

在很多情况下可以快速收敛，但有些函数并不收敛。

误差分析

  1. 使用时需要使初始迭代点$x_0$在$x$附近，$x_0$所控制区间$[a,b]$只有一个根存在$\Rightarrow f(a)$与$f(b)$异号，$f’(x)$在该区间内符号不发生改变（$f(x)$在$[a,b]$单调）。
  2. $|f’|$不能太小，否则取极限一阶导为0与$x$轴无交点。
  3. $|f’’|$不能太大，太大则准确度不够。

记$x$为真正零点，$E_n=|x-x_n|$，$E_{n+1}=|x-x_{n+1}|$，通常情况下误差满足$E_{n+1}≈E_n^2$。

用途

1.求解方程的根

$$
f(x)=6x^7+8x^6+7x^4+5x^2-y\times x,y为一个实数
$$

可以求导得到$f’(x)=42x^6+48x^5+21x^2+10x-y$，可以发现这个函数最多只有一个解且单调递增。

那我们枚举初始迭代点求解$f’(x)=0$即可。

初始迭代点的选取需要玄学经验，此题若选取$y$为负数(方程无解)会陷入死循环。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
double f(double x,double y){
    return 6*p(x,7)+8*p(x,6)+7*p(x,3)+5*p(x,2)-y*x;
}
double f1(double x,double y){//求导,可以发现这个单增
    return 42*p(x,6)+48*p(x,5)+21*p(x,2)+10*x-y;
}
double f2(double x,double y){//导数的导数
    return 252*p(x,5)+240*p(x,4)+42*x;
}
double getpos(double x,double y){
    while(abs(f1(x,y))>eps)
        x=x-f1(x,y)/f2(x,y);
    return x;//牛顿迭代法求f'(x)=0近似解
}
signed main(signed argc, char const *argv[])
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        double y,ans=1e17;
        scanf("%lf",&y);
        for(int i=0;i<=100;i++)
        {
            double newpos=getpos(i,y);
            if(newpos>=0&&newpos<=100)
                ans=min(ans,f(newpos,y));
        }
        printf("%.4f\n",ans);
    }
    return 0;
}
/*
 *求出x在[0,100]上f(x)的最小值
*/
2.开根号

使用牛顿迭代法求解$\sqrt a$，比二分法迭代次数更少。

高中不让用计算器可以用来手动开根号

令$f(x)=x^2-a$，使用牛顿迭代求$f(x)=0$的解。

迭代公式$x_{n+1}=x_n-\dfrac{f(x_n)}{f’(x_n)}=\dfrac{1}{2}(x_n-\dfrac{a}{x_n})$。

常见结论

  • 哥德巴赫猜想
    1. 任何一个不小于4的偶数可以表成两个素数之和
    2. 任何一个不小于7的奇数可以表成三个素数之和。CF735D Taxes
  • 齐肯多夫定理
    1. 任何正整数可以表示为若干个不连续的$fibonacci$数之和

高斯消元

$O(n^3)$求解线性方程组，见图论的矩阵树定理部分